It makes me happy to know that this post will be the one knocking the “Covering Spaces” post off of the front page. This one will cover a related topic but (hopefully) with the noticable difference that while that post is trash, this one will be somewhat well-written. That being said, I’m going to be (mostly) stepping away from the (certain flavor of) number theory that I have been writing about, and make my next few posts more geometric/topological. ¹ Kicking things off, this post will be about showing an equivalence between 3 seemingly different² kinds of objects. I’ll start off by briefly introducing categories and sheaves ³; then I’ll say some things about covers, and finally get into the good stuff.

Categories and Sheaves (Sheafs?)

I’ve wanted to introduce categories on this blog for a long time now, but this is not the context in which I imagined I would do it. ⁴ Anyways, what’s a category?

A (small) category $\mc C$ is a collection (not necessarily a set) $\ob\mc C$ of objects and, for each pair $A,B\in\ob\mc C$ of objects in $\mc C$, a set $\mc C(A,B)=\Hom_{\mc C}(A,B)$ of morphisms such that

If $f\in\Hom_{\mc C}(A,B)$ and $g\in\Hom_{\mc C}(B,C)$ are morphisms, then there is a unique composite morphism $g\circ f\in\Hom_{\mc C}(A,C)$. Furthermore, composition of morphisms is associative so $h\circ(g\circ f)=(h\circ g)\circ f$ whenever either (and hence both) side is defined.
For all $A\in\ob\mc C$, there exists an identity morphism $1_A\in\Hom_{\mc C}(A,A)$ such that, for all $B\in\ob\mc C$ all $f\in\Hom_{\mc C}(A,B)$ and all $g\in\Hom_{\mc C}(B,A)$, we have $f=f\circ1_A$ and $g=1_A\circ g$.

If $f\in\mc C(A,B)$ we will often denote this by writing $f:A\to B$ like we do for normal functions. Finally, let $\Mor\mc C=\bigcup\Hom_{\mc C}(A,B)$ be the collection of all morphisms in $\mc C$.

Our categories are small because we require our hom-sets to be, well, sets instead of allowing (potentially proper) classes like we do for our collection of objects.

The notion of a category is very general; think of your favorite type of mathematical object and you can probably form a category out of these things. The goto first example of a category people see is $\mrm{Set}$, the category whose objects are sets and whose morphisms are set maps. However, while easy to understand, this is a terrible example becasue (1) nobody ever does math in the category $\mrm{Set}$ (sets are too unstructured) and (2) seeing this example makes it harder to internalize the fact that objects/morphisms are atomic as far as category theory is concerned (you’re objects don’t have to be sets, and your morphisms don’t have to be “structure-preserving” set maps). ⁵

As far as fixing (1) above, better examples to have in mind are $\mrm{Top}$, the category of topological spaces with continuous maps are morphisms; $\mrm{Ab}$, the category of abelian groups with group homomorphisms as its morphisms; and $R-\mrm{Mod}$ (here, $R$ is some ring), the category of left $R$-modules ⁶ with $R$-linear maps as its morphisms. For better examples as far as (2) is concerned, think about the following.

Let $G$ be a graph. Convince yourself that this gives rise to a category whose objects are vertices and whose morphisms are edges.

Let $\mc C$ be a category, and let $f:A\rightleftarrows B:g$ be morphisms such that $f\circ g=1_B$ and $g\circ f=1_A$. Then, $f,g$ are called isomorphisms.

Show that a group is the same thing as a category with one object in which every morphism is an isomorphism.

Think of another category whose morphisms are not set-theoretic.

Category theory is all about studying objects through their properties and their interactions (i.e. maps) with other objects of the same type instead of through their particular construction. So if we want to study categories, we should study maps between categories.

Let $\mc C,\mc D$ be two categories. A (covariant) functor $F:\mc C\to\mc D$ is a choice of object $F(A)\in\mc D$ for each object $A\in\mc C$, and a collection of maps $\mc C(A,B)\xto F\mc D(F(A),F(B))$ such that $F(1_A)=1_A$ (i.e. $F$ preserves identites) for all $A\in\mc C$ and $F(f\circ g)=F(f)\circ F(g)$ (i.e. $F$ preserves compositions) for all morphisms $f,g\in\Mor C$ whenever both sides are defined.

If an asignment $F$ reverses arrows (i.e. gives maps $\mc C(A,B)\to\mc D(F(B),F(A))$), then we call is a contravariant functor. Letting $\mc C\op$ denote the category whoses objects are the same as in $\mc C$ and whose morphisms are the same as in $\mc C$ except going the other way around, a contravariant functor $\mc C\to\mc D$ is the same thing as a covariant functor $\mc C\op\to\mc D$.

Many (pairs of) categories have "forgetful functors" that just forget some structure. For examples, there's a forgetful functor $\mrm{Ab}\to\mrm{Set}$ and also one from $R\mrm{-Mod}$ to $\mrm{Ab}$.

Less boringly, the fundamental group $\pi_1$ is a functor $\mrm{Top}\to\mrm{Grp}$. Similarly, $n$th singular cohomology gives a contravariant functor $\mrm{Top}\to\mrm{Ab}$.

Given any $A\in\mc C$, we can form two $\Hom$-functors $\Hom(A,-)$ and $\Hom(-,A)$. It's often beneficial to try and understand an object by understanding its $\Hom$-functors. Note that $\Hom(A,-)$ is covariant while $\Hom(-,A)$ is contravariant. This is often a source of confusion.

Now that we know what a functor is, we can form a (large) category $\mrm{Cat}$ whose objects are (small) categories and whose morphisms are functors, but why stop there? The real raison d’être of category theory is to look at categories whose objects are functors and whose morphisms are $\dots$⁷

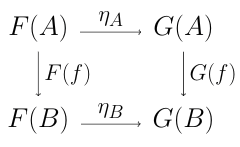
Given two (covariant) functors $F,G:\mc C\to\mc D$, a natural transformation $\eta$ is a collection of maps $\eta_A:F(A)\to G(A)$ such that for all $A,B\in\mc C$ and $f\in\Hom_{\mc C}(A,B)$, we have $G(f)\circ\eta_A=\eta_B\circ F(f)$. i.e. the following square commutes

We denote this by $\eta:F\to G$ or $\eta:F\implies G$.

Now, given two categories $\mc C,\mc D$, we let $\mc D^{\mc C}$ denote the category of (covariant) functors $\mc C\to\mc D$ with natural transformations as morphisms, and let $\mc D^{\mc C\op}$ denote the cateogry of contravariant functors $\mc C\to\mc D$ with natural transformations as morphisms.

I know I joked above about this stuff being abstract nonsense ⁸, but these functor categories are actually fairly natural and show up often; although, they’re not always presented as functor categories.

Let $G$ be a group and $k$ be a field. Recall that we can view $G$ itself as a category. With this in mind, the category of linear $G$-reps in the functor category $k$-Mod$^G$.

A directed graph is two sets - edges and vertices - with two maps from the edge set to the vertex set - source and target - so the category of directed graphs is the functor category Set$^{\mc C}$ where $\mc C$ is the category with 2 objects $A,B$ and 2 morphisms $A\rightrightarrows B$.

Let $X$ be a topological space, and let $\Open(X)$ be the category whose objects are open subsets of $X$ and whose morphisms are inclusion maps $U\into V$ (in particular, each Hom-set as cardinality at most 1). Fix a category $\mc C$. The category of ($\mc C$-valued) presheaves on $X$ is the functor category $\mc C^{\Open(X)\op}$.

Let $X$ be a topological space. Unpacking the above definition, a presheaf $\msP$ on $X$ is, for every open $U\subseteq X$, a choice of $\msP(U)\in\ob\mc C$ such that if $U\subseteq V$ are both open, there is a "restriction" morphism $\rho_{UV}:\msP(V)\to\msP(U)$. We require that $\rho_{UU}=1_{\msP(U)}$ and $\rho_{UV}\circ\rho_{VW}=\rho_{UW}$ for all $U\subseteq V\subseteq W$ open in $X$. We usually write $f\mid_U$ for $\rho_{UV}(f)$ (This is because many important examples of (pre)sheaves are of the form "nice" functions on $U$ where "nice" might mean continuous, smooth, holomorphic, etc.).

A morphism of presheaves $\msP,\msS$ on $X$ is a collection of maps $\msP(U)\to\msS(U)$ commuting with the restriction maps on $\msP,\msS$ respectively.

We’ll say more about (pre)sheaves in a bit, but before that, there’s a little more category theory to introduce. Anytime you define a mathematical object, you have to ask yourself what equivalence relation you want to consider them up to. For categories, there are (at least) 2 choices. The first is fairly obvious.

Two categories $\mc C,\mc D$ are called isomorphic if they are isomorphic in $\mrm{Cat}$. That is, if there exists functors $F:\mc C\rightleftarrows\mc D:G$ such that $F\circ G=1_{\mc D}$ and $G\circ F=1_{\mc C}$.

This turns out to be too strong a condition most of the time, so people usually only care about a weaker condition which you can think of as the homotopy equivalence of categories.

Two categories $\mc C,\mc D$ are called equivalent if there exists functors $F:\mc C\rightleftarrows\mc D:G$ with isomorphisms of functors (i.e. natural transformations with inverse natural transformations) $\eta:G\circ F\implies1_{\mc C}$ and $\eta':F\circ G\implies1_{\mc D}$.

The goal of this post is to show that three certain categories are equivalent. One of these is the category of locally constant sheaves, so let us return to (pre)sheaves. ⁹

Let $\msP$ be a $\mc C$-valued presheaf on a topological space $X$ where $\mc C$ is a category with a forgetful functor to $\mrm{Set}$ (e.g. $\Ab$). Recall that this means that $\msP$ is a contravariant functor $\Open(X)\to\mc C$. We say that $\msP$ is a sheaf if it is "locally defined" in the sense that for any collection $\{U_i\}$ of open sets and elements $f_i\in\msP(U_i)$ satisfying $f_i\mid_{U_i\cap U_j}=f_j\mid_{U_i\cap U_j}$ for all $i,j$, there is a unique $f\in\msP(U)$ with $f\mid_{U_i}=f_i$ for all $i$.

That definition is a bit of a mouthful because I tried to make it general, but then ran into the issue that not all categories are built from sets. To stop further confusion, for the rest of this section assume all presheaves (at the very least) spit out abelian groups because this is (almost) always true in practice anyway ¹⁰. A sheaf is a presheaf where given a consistent choice of elements $f_i\in\msP(U_i)$, you can always (uniquely) glue these to get a global elements $f\in\msP(\bigcup U_i)$. Now, sheaves are really good for studying local properties and studying their ability (or failure) to satisfy local-to-global principals. One notion that helps in studying local properties via sheafs is that of a stalk.

Fix a presheaf $\msP$ on a space $X$, and choose some $x\in X$. Let $U,V\subseteq X$ be (open) neighborhoods in $X$. We say $f\in\msP(U)$ and $g\in\msP(V)$ have the same germ if there's some $W\subseteq U\cap V$ such that $f\mid_W=g\mid_W$. This is an equivalence relation. The stalk $\msP_x$ of $\msP$ at $x$ is the set of germs of sections defined near $x$ (i.e. of $f\in\msP(U)$ for any $U\ni x$).

More algebraically, the stalk of a presheaf is the direct limit $$\msP_x=\dirlim_{x\in U}\msP(U)$$ taken over neighborhoods of $x$.

This post is looking like it might get quite long ¹¹, so I’m just gonna move on without discussing stalks further except to say that, for our needs, they will appear as fibers of certain topological covers.

Sheaves are nice to have and work with, but presheaves are easier to write down. Thus, it’s really nice that there is a (functorial) process called sheafification that, given any presheaf $\msP$ spits out a sheaf $\msP^+$ with a morphism $\msP\to\msP^+$ inducing an isomorphism on stalks ¹² such that any morphism $\msP\to\msS$ from $\msP$ to a sheaf $\msS$ factors uniquely as $\msP\to\msP^+\to\msS$. Let’s end this section with a simple example. Fix an abelian group $M$ and a topological space $X$. Let $M_X$ denote the constant presheaf, i.e. $M_X(U)=M$ for all $U\in\Open(X)$. ¹³ Its sheafification $M_X^+$ is the locally constant sheaf (which, because sheaves > presheaves, we still denote $M_X$ and we refer to as a constant sheaf) whose value on $U\in\Open(X)$ is $M\oplus M\oplus\cdots\oplus M$ where the number of factors of $M$ equals the number of connected components of $U$ ¹⁴. It would not be a bad idea to pause and go through the trouble of varifying that the constant presheaf really is a presheaf whose sheafification really is the constant sheaf as I have defined them.

Covers

Well, that last section felt like a lot of material to introduce all at once, so I really hope you’ve seen categories and/or presheaves before. ¹⁵ I think this one will be more digestible ¹⁶.

Let $X$ be a topological space. A space over $X$ is a topological space $Y$ with a continuous map $p:Y\to X$. A morphisms bewteen two spaces $p_i:Y_i\to X$ ($i=1,2$) over $X$ is a continuous map $f:Y_1\to Y_2$ such that the following triangle commutes

The set $\inv p(x)$ is called the fiber over $x$.

Let $X$ be a topological space. A cover (or covering space) of $X$ is a space $p:Y\to X$ over $X$ such that every point $x\in X$ has a neighborhood $U\ni x$ (called an elementary (or fundamental) neighborhood) such that $\inv p(U)$ is a disjoint union of open sets $\wt U_i$ of $Y$ and $p\mid_{\wt U_i}:\wt U_i\to U$ is a homeomorphism for all $i$.

Given any discrete space $I$, there's a trivial cover $X\by I\to X$ given by projection onto the first factor. More generally, the existence of fundamental neighborhoods means that any cover $p:Y\to X$ is locally trivial in the sense that each point of $X$ has a neighborhood $U$ s.t. $\inv p(U)\simeq X\by I$ (here, this isomorphism is in the category of spaces over $X$, or equivalently, in the category of covers of $X$) for some discrete $I$.

Because covers $p:Y\to X$ are locally trivial fibers are "locally homeomorphic" in the sense that each point $x\in X$ has a neighborhood in which every point's fiber is homeomorphic to $\inv p(x)$. This allows us to conclude that all fibers in any connected component of $X$ are homeomorphic. This remark does not use the discreteness of fibers and in fact holds for more general "fiber bundles" that I will not define here.

Let $p:Y\to X$ be a cover with $X$ connected. The size $\abs{\inv p(x)}$ of any fiber is called the degree of the cover.

Let’s collect some facts about covers.

Let $G$ be a group with a continuous (left) action on a topological space $Y$. We say its action is even (or properly discontinuous) if each point $y\in Y$ has some open neighborhood $U$ such that the sets $gU$ are pairwise disjoint for all $g\in G$.

If $G\actson Y$ evenly, then the natural projection $Y\to G\sm Y$ is a cover.

Let $p:Y\to X$ be a cover and $Z$ a connected topological space. If two maps $f,g:Z\rightrightarrows Y$ satisfy $p\circ f=p\circ g$ (i.e. $f,g$ lift the same map $Z\to X$), then $f,g$ either agree everywhere or nowhere. That is, if there's some $z\in Z$ with $f(z)=g(z)$, then $f=g$.

This was shown in a previous post.

If $p:Y\to X$ is a connected cover, the action of $\Aut(Y\mid X)$, the group of covering morphisms $Y\to Y$ with inverse covering morphisms, on $Y$ is even and free.

Fix any $y\in Y$, and let $x=p(y)$. Let $V\ni x$ be fundamental, so $\inv p(V)$ is a disjoint union of open sets $U_i$, one of which, say $U_j$, contains $y$. Now, fix any $\phi\in\Aut(Y\mid X)$. Then, $p\circ\phi=p$ maps $U_j$ homemorphically onto $V$, and so $\phi(U_j)$ must be one of the $U_i$'s. Hence, the translates $\phi(U_j)$ of $U_j$ are disjoint, so $\Aut(Y\mid X)$ acts evenly. Furthermore, since $p\circ\phi=p$, $\phi(U_j)=U_j$ implies that $\phi(y)=y$ which (by the proposition) implies that $\phi=1_Y$ is the identity map, so $\Aut(Y\mid X)$ acts freely as well.

Let $f:Y\to Z$ be a map between covers of $X$ (i.e. $f$ fits into a commutative triangle with $Y,Z$ both projecting to $X$). Then, $f$ is a cover of $Z$.

At this point, I should probably mention this section is about laying the ground work to show an equivalence of categories between covers of $X$ and $\pi_1(X,x)$-sets for “nice enough” $X$. To define the relavent functor, we’ll need a way to recover a $\pi_1(X,x)$-action from a cover of $X$.

Let $p:\wt X\to X$ be a cover. Given a path $f:I\to X$ and a choice $\st x\in\inv p(f(0))$ of lift of the starting point, there exists a unique path $\st f:I\to\wt X$ starting at $\st x$ and lifting $f$ in the sense that $p\circ\st f=f$. Furthermore, if $g:I\to X$ is homotopic to $f$, then $\st g:I\to\wt X$ lifting $g$ and starting at $\st x$ is homotopic to $\st f$.

This was shown in a previous post.

Let $p:Y\to X$ be a cover and fix some $x\in X$. Then, there is a well-defined action of $\pi_1(X,x)$ on the fiber $\inv p(x)$ given by lifting a loop to a path in $Y$ and then taking its right endpoint.

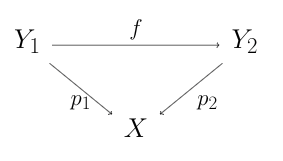
$\DeclareMathOperator{\Cov}{Cov}\DeclareMathOperator{\Fib}{Fib}$ For concreteness, let $\Cov(X)$ denote the category of coverings of $X$, and let $\pi_1(X,x)\mrm{-Set}=\mrm{Set}^{\pi_1(X,x)}$ denote the category of left $\pi_1(X,x)$-sets. We want to say that the above corollary gives the existence of a functor $F=\Fib_x:\Cov(X)\to\pi_1(X,x)\mrm{-Set}$ such that $F(p)=\inv p(x)$. However, we may worry that it is nonobvious that this construction comes with $\pi_1(X,x)$-equivariant induced maps (i.e. natural transformations) $F(f):\inv p_1(x)\to \inv p_2(x)$ where $f:Y_1\to Y_2$ is a cover morphism from $p_1:Y_1\to X$ to $p_2:Y_2\to X$. However, there is nothing to worry about. The obvious choice of $F(f):\inv p_1(x)\to\inv p_2(x)$ is $\pi_1(X,x)$-equivariant because of uniqueness of path lifting.

Convince yourself that $\Fib_x$ defined above actually is a functor.

We’ll show that $\Fib_x$ is an equivalence of categories in the next section. To facilitate this, we’ll show that $\Fib_x$ is representable in the sense that $\Fib_x\cong\Hom_{\Cov(X)}(C,-)$ (this isomorphism taking place in the functor category $(\pi_1(X,x)\mrm{-Set})^{\Cov(X)}$) for some $C\in\Cov(X)$. To make $\Hom_{\Cov(X)}(C,D)$ a $\pi_1(X,x)$-set, give it the post-compose by (the action of) $\gamma\in\pi_1(X,x)$ action.

Let $X$ be path-connected and semilocally simply connected, and fix a base point $x\in X$. Then, the functor $\Fib_x$ is representable by a cover $\wt X_x\to X$.

I think the construction of $\wt X_x$ is one of those things that becomes obviously the right choice after you see it and digest it, but that can be hard to succinctly motivate beforehand, so I won’t try to. As a general rule of thumb, let $I=[0,1]$ denote the unit interval.

Let $\wt X_x=[(I,0)\to(X,x)]$ be the set of homotopy classes (rel basepoints) of paths starting from $x$, and let $p:\wt X_x\to X$ be projection onto the right endpoint. To turn $\wt X_x$ into a space, we endow it with the following topology: given a point $[f]\in\wt X_x$, its neighborhood base consists of sets of the form $$\st U_f:=\bracks{[g\circ f]:g:I\to X, g(0)=y, g([0,1])\subset U}$$ where $U\subseteq X$ is open such that the injection $i:U\into X$ induces the zero map $\push i:\pi_1(U,p([f]))\to\pi_1(X,p([f]))$ (i.e. every path contained in $U$ is contractible via some homotopy in $X$). This is to say that $\st U$ is (homotopy classes) of paths that continue $f$ within $U$. Since we are allowed to take homotopies in $X$, an element of $\st U$ is determined by its endpoints. Now, one can easily verify that these sets form a basis for a topology and that $p$ is continuous with respect to this topology. Note that given a $[f]\in\wt X_x$, and a subspace $i:U\into X$ with $\push i\pi_1(X,f(1))=0$, $\inv p(U)$ consists sets of the form $\st U_f$ for all $[f]\in\pi_1(X,x)$ and so $p$ really is a cover.
Now, fix the point $\st x\in\wt X_x$ to be the homotopy class of the constant loop at $x$. We will show that the cover $p:\wt X_x\to X$ represents the functor $\Fib_x$. This means we need a functorial isomorphism $\inv q(x)\iso\Hom_{\Cov(X)}(\wt X_x,Y)$ for any cover $q:Y\to X$. For any such cover and any choice of $y\in\inv q(x)$, let $\pi_y:\wt X_x\to Y$ be the morphism taking a point $[f]\in\wt X_x$ to $\st f(1)$ where $\st f:[0,1]\to Y$ is the unique path lifting $f$ with $\st f(0)=y$. Note that this is $\pi_1(X,x)$-equivariant by uniqueness of path lifting. To see that this is an isomorphism, observe that the map $\phi\mapsto\phi(\st x)$ is an explicit inverse. Finally this map is functorial since given a morphism $Y\to Y'$ of covers of $X$ taking $y\in Y$ to $y'\in Y'$, the induced map $\Hom_{\Cov(X)}(\wt X_x,Y)\to\Hom_{\Cov(X)}(\wt X_x,Y')$ takes $\pi_y$ to $\pi_{y'}$ as these are the maps sending $\wt x$ to $y$ and $y'$, repsectively.

To make matters simpler, fix some path-connected and semilocally simply connected space $X$ with a choice of basepoint $x\in X$. The representing cover $\wt X_x$ coming from the above theorem is called the universal cover of $X$.

The universal cover $\wt X_x$ is path-connected with automorphism group $\Aut(\wt X_x\mid X)\simeq\pi_1(X,x)$ which acts transtiviely on the fiber above $x$.

Exercise.

At this point, I think we have (almost) everything we need to show that covers of $X$ are the same thing as sets with a $\pi_1(X,x)$-action.

The First Equivalence

You may have noticed the “(almost)” in the previous sentence. That’s there because directly proving a functor gives an equivalence of categories is annoying since you need to give an inverse functor and two natural transformations. To help ease our pain, we’ll prove a lemma which says that the existence of one “nice” functor suffices to prove an equivalence of categories.

A functor $F:\mc C_1\to\mc C_2$ is faithful if the induced map $\mc C_1(A,B)\to\mc C_2(F(A),F(B))$ is injective for all $A,B\in\mc C_1$. If these maps are always bijective, then $F$ is fully faithful.

A functor $F:\mc C_1\to\mc C_2$ is essentially surjective if every $A_2\in\mc C_2$ is isomorphic to $F(A_1)$ for some $A_1\in\mc C_1$.

Two categories $\mc C_1,\mc C_2$ are equivalent if and only if there exists a functor $F:\mc C_1\to\mc C_2$ which is fully faithful and essentially surjective.

We will give a proof of the “if” direction, but leave the “only if” direction as an exercise.

$(\to)$ Assume $F:\mc C_1\to\mc C_2$ is a fully faithful, essentially surjective functor. For each $X\in\mc C_2$, fix an isomorphism $i_X:F(A)\iso X$ for some $A\in\mc C_1$. Let $G:\mc C_2\to\mc C_1$ be the functor sending each $X\in\mc C_2$ to the $A$ chosen above, and each morphism $\phi:X\to Y$ to $$G(\phi)=\inv F(\inv i_Y\circ\phi\circ i_X)$$ which is well-defined since $F$ is fully faithful so its induced map $\Hom(A,B)\to\Hom(F(A),F(B))$ is bijective. The maps $i_X:F(G(V))\iso V$ give an isomorphism $\eta:F\circ G\iso1_{\mc C_2}$ by construction. To finish, we need to give an isomorphism $\eta':G\circ F\iso1_{\mc C_1}$. Hence, we need functorial isomorphisms $\eta'_A:G(F(A))\to A$ for each $A\in\mc C_1$. Since $F$ is fully faithful, it suffices to construct maps $$F(\eta'_A):F(G(F(A)))\to F(A).$$ We take $F(\eta'_A)=\eta_{F(A)}$ which is indeed a functorial isomorphism because $\eta$ is an isomorphism in $\mrm{Cat}$. Thus, we win.

I bet you can guess what comes next: to show that $\Fib_x$ gives an equivalence of categories, we’ll show that it is fully faithful and essentially surjective. We’ll prove each of these as a lemma, and then conclude what we want. Fix some path-connected and semilocally simply connected topological space $X$ with a chosen basepoint $x\in X$.

$\Fib_x$ is fully faithful.

Let $p:Y\to X$ and $q:Z\to X$ be two covers of $X$. We need to show that each map $\phi:\Fib_x(Y)\to\Fib_x(Z)$ of $\pi_1(X,x)$-sets comes from a unique map $Y\to Z$ of covers of $X$. We can assume that $Y,Z$ are connected (else run this argument on pairs of connected components). Let $\wt X_x$ be the universal cover of $X$, and recall the maps $\pi_y:\wt X_x\to Y$ defined for each $y\in Y$. Let $U_y=\Aut(\wt X_x\mid Y)$ be the stabilizer of $y$, and note that $\pi_y$ descends to a map $U_y\sm\wt X_x\to Y$ since the action of $U_y$ fixes fibers above $y$. This map is a homeomorphism (and hence a cover isomorphism once $U_y\sm\wt X_x$ is given the appropriate projection map to $X$) since you can define an inverse map $\phi_y:Y\to U_y\sm\wt X_x$ by taking $y'\in Y$ to any lift in $\wt X_x$ and then projecting that lift into $U_y\sm\wt X_x$ (This map is obviously-well defined and a set-theoretic inverse to $\phi$. Showing that it's continuous is left as an exercise). Now, $U_y$ injects into the stabilizer of $\phi(y)$ via $\phi$, so the natural map $\pi_{\phi(y)}:\wt X_x\to Z$ induces a map $$U_y\sm\wt X_x\to U_{\phi(y)}\sm\wt X_x\iso Z.$$ Composing this with the map $\phi_y:Y\iso U_y\sm\wt X_x$ gives the desired map $Y\to Z$.

$\Fib_x$ is essentially surjective.

We need to show that each left $\pi_1(X,x)$-set $S$ is isomorphic to the fiber of some cover of $X$. We can assume that $\pi_1(X,x)$ acts transitively on $S$ (else take the disjoint union of the covers corresponding to each orbit), so let's assume that. Fix any $s\in S$, and let $H=\pi_1(X,x)_s$ be its stabilizer. Since $H\le\pi_1(X,x)\simeq\Aut(\wt X_x\mid X)$, we can consider the quotient $H\sm\wt X_x$. This is our desired cover of $X$.

The categories $\Cov(X)$ of covers of $X$ and $\mrm{Set}^{\pi_1(X,x)}$ of sets with a $\pi_1(X,x)$-action are equivalent.

Let $\wh{\pi_1(X,x)}$ denote the profinite completion of $\pi_1(X,x)$ (i.e. $\invlim\pi_1(X,x)/N$ where $N$ ranges over normal subgroups of finite index partially ordered by inclusion). Prove that $\Fib_x$ induces an equivalence of categories between the category of finite covers of $X$ (i.e. covers with finite fibers) and sets with a continuous left $\wh{\pi_1(X,x)}$-action.

Whelp. I hope the journey was worth it. Probably if you’ve seen covering spaces before, this isn’t too surprising, but I think it’s still nice to see things from a more categorical perspective. I suspect that the next result is will be more surprising even to someone who has seen sheaves before (unless, of course, they’ve also seen this result before) ¹⁷: the category of (left) $\pi_1(X,x)$-sets is equivalent to the category of locally constant sheaves on $X$.

The Second Equivalence

Let’s get started. First off, I don’t think I mentioned this before (but I did use this terminology earlier), but if $\ms P$ is a presheaf and $U\subseteq X$ is open, then any $s\in\msP(U)$ is called a section of $\msP$ (defined) over $U$. This is because “sheaves of sections” (this use of “section” refering to (local) right inverses) show up fairly regularly in math ¹⁸. As an example

Let $p:Y\to X$ be a space over $X$ (note: not necessarily a cover), and $U\subset X$ an open set. A section of $p$ over $U$ is a continous map $s:U\to Y$ such that $p\circ s=1_U$.

Let $p:Y\to X$ be a space over $X$, and let $\ms F_Y$ be the $\mrm{Set}$-valued presheaf on $X$ of sections of $p$. i.e. $$\ms F_Y(U)=\bracks{s:U\to Y:p\circ s=1_U},$$ and the restriction maps $\ms F_Y(U)\to\ms F_Y(V)$ for an inclusion $V\into U$ are literally given by restricted a section to a subspace. This presheaf is actually a sheaf essentially because continuous functions are locally definable (use the pasting lemma).

Now, recall that a constant sheaf $\msS=S_X$ is the sheafification of the presheaf of constant functions to some fixed set $S$ (i.e. $\msS(U)$ is the set of locally constant functions $U\to S$). You may object that these should really be called locally constant sheaves; I hear that objection, ignore it, and make the following definition just to make the situation more confusing.

A sheaf $\msS$ on a topological space $X$ is locally constant if each point of $X$ has an open neighborhood $U$ such that $\msS\mid_U$ (the restriction of $\msS$ to $U$ which is a sheaf on $U$) is isomorphic (in the category of sheaves on $U$) to a constant sheaf.

Let $p:Y\to X$ be a cover with $X$ connected. Then, the sheaf $\ms F_Y$ of sections is locally constant, and is constant if $p$ is trivial (i.e. a homeomorphism).

Given some $x\in X$, let $V$ be one of its fundamental neighborhoods. The image of a section $V\to Y$ must be one of the connected components of $\inv p(V)$, so sections over $V$ correspond bijectively to points of the fiber $\inv p(x)$. Hence, $\ms F_Y\mid_V$ is (isomorphic to) the constant sheaf $F_X$ defined by $F=\inv p(x)$. $\ms F_Y$ itself is constant if and only if we may take $V=X$ if and only if $p$ is trivial.

Let $p:Y\to X$ be a cover and fix any $x\in X$. Then the stalk $\ms F_{Y,x}$ of $\ms F_Y$ at $x$ is (isomorphic to) the fiber $\inv p(x)$.

I don't think I ever wrote down an example of a cover, so let's do that now. View $S^1\subseteq\C$ as the unit circle. Then, the $n$th-power map $z\mapsto z^n$ gives a degree $n$ cover $S^1\to S^1$. For all $n>1$, this cover is nontrivial and hence, by the above, gives rise to a locally constant but non-constant sheaf.

$\DeclareMathOperator{\LCS}{LCS}$ Note that a morphism $\phi:Y\to Z$ of covers of $X$ induces a morphism $\ms F_Y\to\ms F_Z$ of locally constant sheaves by taking the local section $s:U\to Y$ to $\phi\circ s$ ($\phi\circ s$ is a local section precisely because $\phi$ is a cover morphism) ¹⁹. Hence, we get a functor $S:Y\mapsto\ms F_Y$ from the category $\Cov(X)$ of covers of $X$ to the category $\LCS(X)$ of $\mrm{Set}$-valued locally constant sheaves on $X$. To show that this functor gives an equivalence of categories we’ll just construct an inverse this time. This is where we get to make use of stalks.

Let $X$ be a topological space, and let $\ms F$ be a presheaf (of sets) on $X$. Let $X_{\ms F}=\bigsqcup_{x\in X}\ms F_x$ be the disjoint union of the stalks of $\ms F$. We want to give this set a topology. Note that for any open $U\subset X$, a section $s\in\ms F(U)$ gives rise to a map $i_s:U\to X_{\ms F}$ sending each $x\in U$ to the germ $s_x\in\ms F_x$ of $s$ over $x$. Give $X_{\ms F}$ the coarsest (i.e. smallest) ²⁰ topology in which the sets $i_s(U)$ are open for all $U$ and $s$. Let $p_{\ms F}:X_{\ms F}\to X$ be the map sending a germ to the point over which it is defined (i.e. $p_{\ms F}\mid_{\ms F_x}=x$ for all $x\in X$). This map is continuous because $\inv p_{\ms F}(U)=\bigcup_{s\in\ms F(U)}i_s(U)$ is open. Furthermore, the maps $i_s:U\to X_{\ms F}$ are continuous as well, and I’ll leave this for you to check. Note that a morphism $\phi:\ms F\to\ms G$ of presheaves induces maps $\ms F_x\to\ms G_x$ for each $x\in X$, and hence a set map $\phi:X_{\ms F}\to X_{\ms G}$ compatible with the projections onto $X$. Thus, the assignment $\ms F\mapsto X_{\ms F}$ gives a functor from the category of sheaves on $X$ to the category of spaces over $X$ (Technically, we need to show that $\phi$ is continuous, but this is easy).

The assignment $C:\ms F\mapsto X_{\ms F}$ restricts to a functor $\LCS(X)\to\Cov(X)$.

By the discussion above the claim, it suffices to show that $p_{\ms F}:X_{\ms F}\to X$ is a cover when $\ms F$ is locally constant. Fix any $x\in X$, and let $U\ni x$ be a neighborhood such taht $\ms F\mid_U$ is constant. Say $\ms F\mid_U\cong F_U$ for some set $F$. Then, $\ms F_x=(\ms F\mid_U)_x=(F_U)_x=F$ for all $x\in U$, so $\inv p_{\ms F}(U)\cong U\by F$ where $F$ is given the discrete topology.

Now that we have our inverse functor, we prove.

Let $X$ be a topological space. Then the functors $S,C$ induce an equivalence of categories between $\Cov(X)$ and $\LCS(X)$.

Let $\ms F$ be a locally constant sheaf, and let $p:Y\to X$ be a cover. We need to show that we have $\ms F_{X_{\ms F}}\cong\ms F$ and $X_{\ms F_Y}\cong Y$ both functorially in $\ms F,Y$ respectively. The map $\ms F\to\ms F_{X_{\ms F}}$ is given by sending a section $s\in\ms F(U)$ to the local section $i_s:U\to X_{\ms F}$ while the map $Y\to X_{\ms F_Y}$ is given by sending a point $y\in Y$ to the corresponding point of the stalk/fiber $\ms F_{Y,p(y)}=\inv p(p(y))$ (Secretly, we fixed some choice of isomorphisms at the beginning of this argument) over $p(y)$. To show that these maps are isomorphisms, it suffices to show that their restrictions over a suitable open covering of $X$ are, so choose a cover $\{U_i\}_{i\in I}$ such that $\ms F\mid_{U_i}$ is constant for each $i$. Replacing $X$ by $U_i$, we may henceforth (not sure if I've ever used this word in a proof before) assume $\ms F\cong F_X$ is a constant sheaf. In this case, $X_{\ms F}\cong X_{F_X}\cong X\by F$, and the sheaf of local sections of the trivial cover $X\by F\to X$ is the constant sheaf $F_X$, so the maps $\ms F\to\ms F_{X_{\ms F}}$ (i.e. $F_X\to\ms F_{X\by F}$) and $Y\to X_{\ms F_Y}$ (i.e. $X\by F\to X_{F_X}$) are isomorphisms, and we win.

Let $X$ be a path connected and locally simply connected topological space, and let $x$ be a point in $X$. Then, $\pi_1(X,x)\mrm{-Set}$ is equivalent to $\LCS(X)$, and this equivalence is induced by the functor $\ms F\to\ms F_x$.

There you have it. A locally constant sheaf on a space $X$ is nothing more than a cover of that space or, if it is nice enough, a (left) $\pi_1(X,x)$-set. To end this post, try proving the following

Let $X$ be path connected and locally simply connected, and fix some basepoint $x\in X$. Let $R$ be a commutative ring. Then, the category of locally constant sheaves of $R$-modules on $X$ is equivalent to the category of (left) modules over the group ring $R[\pi_1(X,x)]$.

For motivation for why you might care about this, fix a field $k$, and recall that a linear representation $\rho:\pi_1(X,x)\to\GL_n(k)$ of the fundamental group of $X$ is the same thing as a choice of a $k[\pi_1(X,x)]$-module $M$ (i.e. there’s an equivalence of categories between linear representations and modules over the group ring). With this in mind, the above exercise asks you to show that a locally constant sheaf of $k$-modules on a (sufficiently nice) space $X$ is the same thing as a representation of its fundamental group! ²¹

As a rule of thumb, if I ever say that I will write a post about something, you probably shouldn’t believe that I will actually follow through with that promise. ↩
Admittedly, the first two are unsurprisingly related ↩
If you know what these are, just skip the first section or two ↩
Always thought it would be in some blog post about $R$-modules and I thought I would not be doing you the disservice of talking about categories without mentioning universal properties. Oh well… it just goes to show ↩
The irony (or not irony? What does this word even technically mean?) of $\mrm{Set}$ technically being the first example I give is not lost on me. ↩
The category of right $R$-modules is written $\mrm{Mod}-R$. ↩
There’s a reason people call this stuff abstract nonsense ↩
If you don’t remember me doing this, then you really gotta start reading these footnotes ↩
You might be wondering if one can define sheaves for categories without forgetful functors to Set. I imagine that the answer to this is yes and that one way to do this is by viewing the elements of an object $A$ in you category as the morphisms $B\to A$ for various $B$ a la this. Alternatively, maybe you can do something like say $\msP$ is a sheave if given any collection $\bracks{U_i}$ for $i\in I$ of open sets, the category whose objects are $\msP\parens{\bigcap_{j\in J}U_j}$ for finite $J\subseteq I$ has all colimits (in the categorical sense). I haven’t thought about this enough to know if either of these work (or if they recover the usual definition when the objects in your category secretly are sets) ↩
When we get into the meat of things, we’ll actually be looking at $\mrm{Set}$-valued sheaves ↩
We’re still in the prelims (!) ↩
Exercise convince yourself that any morphism $\ms A\to\ms B$ between presheaves induces a morphism $\ms A_x\to\ms B_x$ on stalks. ↩
Think of this as the presheaf of constant functions $X\to M$. ↩
i.e. $M_X(U)=M^{\oplus\dim\hom_0(U,\R)}$ ↩
I’m starting to understand why people write textbooks instead of just trying to jam everything into individual blog posts. Maybe I should take a page from Jeremy Kun’s playbook and start separating all the background material into their own separate posts. ↩
I’m assuming you’ve seen fundamental groups before, so probably you’ve also seen covering spaces and this section is mostly review ↩
My introduction to sheaf theory was somewhat nonstandard, so it’s possible that this is a commonly taught/known result and I just happened to be out of the loop until recently ↩
e.g. when proving that the category of vector bundles on a space is equivalent to the category of locally free sheaves on that space ↩
Show rigorously that this is a well-defined map of sheaves (hint: because these things are sheaves to show that $\phi\circ s$ is a section, it suffices to show that it restricts to a section on each set in an open cover of $U$) ↩
I don’t think I’ll ever be able to remember which of “coarser” and “finer” means smaller without pulling up Wikipedia. ↩
(I’m pretty sure that) It is possible to recover a group from its category of $k$-linear representations, so perhaps if you wanted to define a version of the fundamental group in algebraic contexts where you have a not-so-nice topology, you should try giving a definition in terms of locally constant sheaves of that space (or in terms of covers of that space). ↩

Thoughts of a Programmer

Code, Math, Maybe some other stuff

Covering Spaces, $\pi_1$-actions, and Locally Constant Sheaves

Categories and Sheaves (Sheafs?)

Covers

The First Equivalence

The Second Equivalence