In this post, I want to focus on the Riemman $\zeta$ function, and (one type of) its generalizations: the Dirichlet $L$-functions. We’ll prove some nice properties of these things (e.g. their meromorphic continuations, product formulas, and functional equations), and use them to prove some infinitude results involving primes (spoiler: we’ll show e.g. that there are infinitely many primes!).

Riemann

The Riemann Zeta Function is defined as $$\zeta(s)=\sum_{n\ge1}\frac1{n^s},$$ where $s\in\C$. Note that this converges absolutely when $\Re(s)>1$ (e.g. by the integral test).

We want to show that, among other things, this function extends to a meromorphic function on the entire complex plane. To begin, we’ll show that it’s at least holomorphic in the half-plane $\Re(s)>1$ by appealing to a standard theorem from complex analysis ¹.

Let $\{f_n\}_{n=1}^\infty$ be a sequence of holomorphic functions that converges uniformly to a function $f$ in every compact subset of an open set $\Omega\subseteq\C$. Then, $f$ is holomorphic in $\Omega$. Furthermore, the sequence of derivatives $\{f_n'\}_{n=1}^\infty$ converges uniformly to $f'$ on every compact subset of $\Omega$.

$\zeta(s)$ defines a holomorphic function in the half-plane $\Re(s)>1$.

Next, we’ll derive the product formula for the $\zeta$ function. Morally, we want to perform the following manipulation (where $p$ always denotes a prime because we’re not savages)$\dots$

\[\sum_{n\ge1}\frac1{n^s}=\sum_{n\ge1}\prod_{p\mid n}\frac1{p^{sv_p(n)}}=\prod_p\sum_{n\ge0}\frac1{p^{sn}}=\prod_p\parens{\frac1{1-p^{-s}}}.\]

Above, $v_p(n)$ is the number of times the prime $p$ divides the number $n$. The middle equality is (formally) justified by the fundamental theorem of arithmetic; every number has a unique factorization into primes and this corresponds to picking some exponent for each prime ². The above is called an Euler product because Euler was the first person to show this equality, but I think his argument was about as legitimate as what I wrote above, so let’s do one better and actually prove this.

The Euler product for the Riemann Zeta function is legit (at least for $\Re(s)>1$).

We'll do the classic analysis thing and prove that the Euler product is at most $\zeta(s)$, and that it is at least $\zeta(s)$.
$(\le)$ Fix some positive integer $N\ge1$. Then, by the fundamental theorem of arithmetic, we have $$\prod_{p\le N}\sum_{n=0}^N\frac1{p^{sn}}=\sum_{n\in S}\frac1{n^s}\le\sum_{n=1}^\infty\frac1{n^s}=\zeta(s),$$ where $S=\bracks{n:p\le N\implies v_p(n)\le N\text{ and }p>N\implies v_p(n)=0}$. Taking the limit as $N\to\infty$ gives $$\prod_p\sum_{n\ge1}\frac1{p^{sn}}=\prod_p\parens{\frac1{1-p^{-s}}}\le\zeta(s),$$ which has the added benefit of showing the Euler product converges.
$(\ge)$ Fix some positive integer $N\ge1$. Then, $$\sum_{n=1}^N\frac1{n^s}\le\prod_{p\le N}\sum_{n=0}^N\frac1{p^{ns}}\le\prod_p\sum_{n=0}^\infty\frac1{p^{ns}}.$$ Taking the limit as $N\to\infty$ gives $$\zeta(s)\le\prod_p\parens{\frac1{1-p^{-s}}}$$ as desired.

There are infinitely many primes.

$$\lim_{s\to1^+}\prod_p\parens{\frac1{1-p^{-s}}}=\lim_{s\to1^+}\zeta(s)=\lim_{s\to1^+}\sum_{n\ge1}\frac1{n^s}.$$ Now, if there are only finitely many primes, then the LHS obviously coverges because it's just a finite product. On the other hand, the RHS obviously diverges since it approaches the harmonic series. Thus, there must be infinitely many primes.

This is largely unrelated to the rest of this post, but whatever; this is my blog so I can go on mini-rants whenever I want. The standard proof that there are infinitely many primes (the one due to Euclid) is not a proof by contradiction even though it's often presented this way. There's no reason to assume that there are finitely many primes in the beginning, becuase you're secretly just constructing an infinite sequence of prime numbers.
i.e let $p_1=2$, and for $n>1$, let $p_n$ be the smallest prime factor of $p_1p_2\cdots p_{n-1}+1$. Then, $p_n$ is prime for all $n$, and $n\neq m\implies p_n\neq p_m$, so this gives an infinite sequence of primes. No contradiction necessary.

While we’re on the subject of primes, we can actually do more than just count them.

$$\sum_p\frac1p=\infty.$$

This is gonna be a little handwavy, but don't worry about that too much; Euler wouldn't (if it helps, mentally restrict $s$ to being real). First recall that $\log(1+x)=\sum_{n\ge1}(-1)^{n+1}x^n/n$ when $\abs x< 1$. Now, note that $$\log\zeta(s)=\log\prod_p\parens{\frac1{1-p^{-s}}}=-\sum_p\log\parens{1-p^{-s}}=\sum_p\sum_{n\ge1}\frac1{np^{ns}}=\parens{\sum_p\frac1{p^s}}+\sum_p\sum_{n\ge2}\frac1{np^{ns}}.$$ Because $$\sum_p\sum_{n\ge2}\frac1{p^{ns}}=\sum_p\sum_{n\ge2}\parens{p^{-s}}^n=\sum_p\frac{p^{-2s}}{1-p^{-s}}\le\frac1{1-2^{-s}}\sum_pp^{-2s}\le2\zeta(2)$$ is bounded as $s\to1^+$, but $\log\zeta(s)$ isn't bounded as $s\to1^+$, we must have $$\sum_p\frac1p=\infty$$ as claimed.

We next move on to analytically continuing the $\zeta$ function. I wish I could give some good motiviation for the argument, but sadly, I cannot. The main idea is to relate the $\zeta$ function to the theta function from last time

\[\vartheta(s)=\sum_{n=-\infty}^\infty e^{-\pi n^2s}\]

and then translate the equality $\vartheta(s)=s^{-1/2}\vartheta(1/s)$ into a similar functional equation for the $\zeta$ function. How do you think up this approach? I don’t know. ³

Before the proof, recall the Gamma function

\[\Gamma(s)=\int_0^\infty e^{-t}t^s\d t/t\]

which is initally defined for $\Re(s)>0$ but extends to a meromorphic function on $\C$ with simple poles at the non-positive integers. The idea here is that integration by parts gives $\Gamma(s+1)=s\Gamma(s)$, so

\[F_m(s)=\frac{\Gamma(s+m)}{(s+m-1)(s+m-2)\cdots s}\]

gives a meromorphic extension of $\Gamma$ to the half plane $\Re(s)>-m$. We can relate $\zeta(s)$ to $\vartheta(s)$ through $\Gamma(s)$ via the following equality:

\[\int_0^\infty e^{-\pi n^2u}u^{s/2}\frac{\d u}u=\pi^{-s/2}\Gamma(s/2)n^{-s},\text{ }\text{ }\text{ }n\ge1.\]

This is seen by making the change of variables $u=\frac t{\pi n^2}$ on the LHS. Motivated by this, call $\xi(s)=\pi^{-s/2}\Gamma(s/2)\zeta(s)$ the xi function ⁴.

$\xi$ has a meromorphic continuation to the entire complex plane, and satisfies the function equation $$\xi(s)=\xi(1-s).$$

Below, the interchange of a sum and integral is (I think) justified because the summands are rapidly decreasing functions. First note that $$\begin{align*} \xi(s) =\int_0^\infty\pi^{-s/2}e^{-t}t^{s/2}\zeta(s)\frac{\d t}t &=\int_0^\infty\sum_{n\ge1}\frac{\pi^{-s/2}e^{-t}t^{s/2}}{n^s}\frac{\d t}t\\ &=\sum_{n\ge1}\int_0^\infty\frac{\pi^{-s/2}e^{-t}t^{s/2}}{n^s}\frac{\d t}t\\ &=\sum_{n\ge1}\pi^{-s/2}\Gamma(s/2)n^{-s}\\ &=\sum_{n\ge1}\int_0^\infty e^{-\pi n^2u}u^{(s/2)}\frac{\d u}u\\ &=\int_0^\infty u^{s/2}\sqbracks{\sum_{n\ge1}e^{-\pi n^2u}}\frac{\d u}u\\ &=\frac12\int_0^\infty u^{s/2}\sqbracks{\vartheta(u)-1}\frac{\d u}u . \end{align*}$$ Not let $\psi(u)=\frac12(\vartheta(u)-1)$, so $$\psi(u)=\frac12\parens{u^{-1/2}\vartheta(1/u)-1}=\frac12\parens{u^{-1/2}\parens{2\psi(1/u)+1}-1}=u^{-1/2}\psi(1/u)+\frac12u^{-1/2}-\frac12.$$ This let's us calculate $$\begin{align*} \xi(s) &=\int_0^\infty u^{s/2}\psi(u)\frac{\d u}u\\ &=\int_0^1u^{s/2}\psi(u)\frac{\d u}u+\int_1^\infty u^{s/2}\psi(u)\frac{\d u}u\\ &=\int_0^1u^{s/2}\sqbracks{u^{-1/2}\psi(1/u)+\frac12u^{-1/2}-\frac12}\frac{\d u}u+\int_1^\infty u^{s/2}\psi(u)\frac{\d u}u . \end{align*}$$ Now, we can make the substitution $u\mapsto1/u$ in the (leftmost summand of the) left integral to transform it into an integral from $1$ to $\infty$. Doing this and calculating the rest of that integral gives $$\begin{align*} \int_0^1u^{(s-1)/2}\psi(1/u)\frac{\d u}u &&&=\int_1^\infty\frac{\psi(u)}{u^{(s-1)/2}}\frac{\d u}u\\ \frac12\int_0^1u^{(s-1)/2}\frac{\d u}u &=\sqbracks{\frac{u^{(s-1)/2}}{s-1}}_0^1 &&= \frac1{s-1}\\ -\frac12\int_0^1u^{s/2}\frac{\d u}u &=-\sqbracks{\frac{u^{s/2}}s}_0^1 &&= \frac{-1}s . \end{align*}$$ Combining this with our expression for $\xi(s)$ above gives $$\xi(s) = \frac1{s-1}-\frac1s+\int_1^\infty\sqbracks{u^{(1-s)/2}+u^{s/2}}\psi(u)\frac{\d u}u.$$ Because $\psi$ decays rapidly (exponentially), the integral defines an entire function, so $\xi$ has an analytic continuation to all of $\C$ with simple poles at $s=0$ and $s=1$. Furthermore, the above expression is unchanged if we replace $s$ by $(1-s)$, so $\xi(s)=\xi(1-s)$ as desired.

The zeta function has a meromorphic continuation to the entire plane with a single simple pole at $s=1$.

We can meromorphically continue $\zeta$ via the equation $$\zeta(s)=\pi^{s/2}\frac{\xi(s)}{\Gamma(s/2)}.$$ Since $1/\Gamma(s/2)$ is entire with simple zeros at the non-positive even integers, we see that simple pole of $\xi(s)$ at $s=0$ cancels out, leaving $\zeta$ with only one simple pole at $s=1$. Furthermore, we see that $\zeta(-2n)=0$ for $n\in\Z_{>0}$.

Expanded out, the functional equation for $\zeta(s)$ is $$\pi^{-s/2}\Gamma\parens{\frac s2}\zeta(s)=\pi^{\frac{s-1}2}\Gamma\parens{\frac{1-s}2}\zeta(1-s).$$

It may be worth noting that the product formula shows that there are no zeros with $\Re(s)>1$, and combining this with the above functional equation shows that the only zeros with $\Re(s)<0$ are at the negative even integers $s=-2k$ with $k\in\Z_{\ge1}$. Thus, any “non-trivial” zero of the Zeta function must lie n the strip $0\le\Re(s)\le1$. This leads me to make the following totally 100% original conjecture:

Ignoring the negative even integers, the only zeros of the Riemman zeta function lie on the line $\Re(s)=\frac12$.

Dirichlet

Dirichlet studied his $L$-series with one specific application in mind: proving that for any coprime $a,n$, there are infinitely many primes $p\equiv a\pmod n$ ⁵. At its core, the idea behind the proof is to follow in Euler’s footsteps by showing that

\[\lim_{s\to1^+}\sum_{p\equiv a\pmod n}\frac1{p^s}=\infty.\]

Unsurprisingly, we will prove this by exploiting some analytic properties of a functions that are reminiscent of $\zeta(s)$.

This summation is similar to $\zeta(1)$, so, letting $\mbf1_ a:\Z\to\bits$ be the characterstic function of congruence to $a\pmod n$, we may be tempted to consider the function $\sum_{n=1}^\infty\mbf1_a(n)n^{-s}$. However, $\mbf1_a$ is not multiplicative, so we’d have a hard time recovering an Euler product for this; since Euler products were useful in proving the infinitue of primes, we’d like to still have one of those. On the bright side, $\mbf1_a$ descends to a homomorphism $\units{(\zmod n)}\to\C$.

A character $\chi$ of the group $G=\units{(\zmod N)}$ is a homomorphism $\chi:G\to\units\C$.

Because of the condition that $\chi(x^{\phi(N)})=\chi(1)=1$, every character actually lands in $S^1\subset\units\C$. More conceptually, because the torsion elements of $\units\C$ are precisely the roots of unity, the characters (of any finite group) can equivalently be defined as homomorphisms $G\to S^1$.

Our first goal is to relate these characters to $\mbf1_a$, our real function of interest. First, note that any character $\chi:\units{(\zmod N)}\to\C$ can be extended to a function $\Z\to\C$ via

\[\chi(n)=\twocases{\chi(n\bmod N)}{\gcd(n,N)=1}0\]

Furthermore, these extensions are completely multiplicative in the sence that $\chi(nm)=\chi(n)\chi(m)$ for all $n,m\in\Z$. To relate this extension to $\mbf1_a:\Z\to\bits\subset\C$, we’ll take a shallow dive in general character theory ⁶.

Shallow Dive

Fix a finite abelian group $G$. By a character on $G$, we mean a homomorphism $G\to S^1$.

The dual group of $G$ is the group $\hat G:=\Hom(G,S^1)$ of characters on $G$.

If $G$ is cyclic of order $n$, then $G\simeq\hat G$ where the isomorphism is non-canonical. This is because a character $\chi:G\to S^1$ is the same thing as a choice of $n$th root of unity in this case, so $\hat G$ is isomorphic to the group of $n$th roots of unity, which is cyclic of order $n$.

Let $H\le G$. Then, every character of $H$ extends to a character of $G$.

Induct on the index $[G:H]$. If $[G:H]=1$, then we're in business. Otherwise, pick some $x\in G\sm H$, and fix $n$ minimal such that $x^n\in H$. Let $t=\chi(x^n)$ and note that we can choose some $w\in S^1$ such that $w^n=t$. Now, let $H'$ be the subgroup of $G$ generated by $H$ and $x$, so any $h'\in H$ can be written $h'=hx^a$ with $a\in\Z$ and $h\in H$. Set $\chi'(h')=\chi(h)w^a$ which gives a (well-defined) character $\chi':H'\to S^1$ extending $\chi$. Since $[G:H']<[G:H]$, we win by induction.

Restricting a character to a subgroup defines a homomorphism $\rho:\hat G\to\hat H$. The above proposition says that $\rho$ is surjective. Since the kernel of $\rho$, characters of $G$ which are trivial on $H$, is isomorphic to $\wh{G/H}$, we obtain a short exact sequence $$1\to\wh{G/H}\to\hat G\to\hat H\to1.$$

Combining the two remarks and the proposition above in a simple induction argument gives the following.

$G\simeq\hat G$ (non-canonically)

Induct on $n$, the order of $G$. If $n=1$, we win, so suppose $n>1$. Let $H\le G$ be a nontrivial cyclic subgroup, so $H\simeq\hat H$ be a previous remark, and $G/H\simeq\wh{G/H}$ by induction. Fixing isomorphisms $\phi,\psi$, we obtain a commutative diagram with exact rows

where the middle vertical map is well-defined because of the existence of the other two maps. Furthermore, this middle map is an isomorphism by the snake lemma (or short 5 lemma or regular 5 lemma) or by an explicit diagram chase.

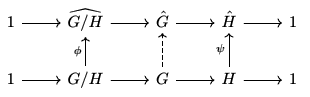
We can actually say something stronger in the case of double duals.

$G\simeq\hat{\hat G}$ where the isomorphism is now canonical.

Consider the map $\eps:G\to\hat{\hat G}$ given by $\eps(x)(\chi)=\chi(x)$. We claim this is an isomorphism. It is clearly a homomorphism. Since we know $G\simeq\hat{\hat G}$ non-canonically, they have the same (finite) order so it suffices to show that $\eps$ is injective. That is to say, if $x\in G$ is $\neq1$, then there exists a character $\chi$ of $G$ such that $\chi(x)\neq1$. To see this, consider $H$, the cyclic subgroup generated by $x$, and note that $H$ has a character $\chi$ such that $\chi(x)\neq1$. Since this character extends to one on $G$, we win.

Finally, we arrive at our last result of this mini-section.

Let $n=\abs G$, and let $\chi\in\hat G$. Then, $$\sum_{x\in G}\chi(x)=\twocases n{\chi=1}0.$$

This obviously holds if $\chi=1$, so suppose $\chi\neq1$. Fix some $y\in G$ such that $\chi(y)\neq1$. Then, $$\chi(y)\sum_{x\in G}\chi(x)=\sum_{x\in G}\chi(xy)=\sum_{x\in G}\chi(x),$$ so $$(\chi(y)-1)\sum_{x\in G}\chi(x)=0.$$ Since $\chi(y)\neq1$, we obtain our desired result.

Fix $x\in G$. Then, $$\sum_{\chi\in\hat G}\chi(x)=\twocases n{x=1}0.$$

The corollary is just applying the theorem to $\hat G$.

Back to Dirichlet

Ok, back to Dirichlet. Remember that we want to relate $\mbf1_a:\Z\to\C$, the characteristic function of being $\equiv a\pmod N$. to characters of the group $\units{(\zmod N)}$. This will be an application of the last theorem from our dive into character theory. First, to make things notationally easier, define $U(N)=\units{(\zmod N)}$ and $X(N):=\wh{U(N)}$.

For all $n\in\Z$, we have $$\mbf1_a(n)=\sum_{\chi\in X(N)}\frac{\chi(a)^{-1}}{\phi(N)}\chi(n).$$

Remember that these characters extend to completely muliplicative functions on the integers, so the right hand side above is really $$\frac1{\phi(N)}\parens{\sum_{\chi\in X(N)}\chi(\inv an)}.$$ The term in the parantheses is $0$ if $\inv an\not\equiv1\pmod N$ and is $\phi(N)$ if $\inv an\equiv1\pmod N$. Hence we win.

Hence, to understand

\[\sum_{p\equiv a\pmod N}\frac1p=\sum_p\frac{\mbf 1_a(p)}p,\]

it should suffice to study the Dirichlet $L$-series defined below.

Fix a character $\chi\in X(N)$. The Dirichlet $L$-series attached to $\chi$ is $$L(\chi, s)=\sum_{n\ge1}\frac{\chi(n)}{n^s},$$ where $s\in\C$. Since $\abs{\chi(n)}=1$, this converges absoluately when $\Re(s)>1$.

A character $\chi\in X(N)$ is called primitive if there does not exist an $N'< N$ and character $\chi'\in X(N')$ such that $\chi(n)=\chi'(\bar n)$ where $\bar n\in\zmod{N'}$ denotes $n$'s reduction modulo $N'$.

Note that the trivial character $\chi=1$ has $\zeta(s)$ as its $L$-series (when $N=1$).

Fix some (primitive) character $\chi\in X(N)$ with $N>1$ (so $\chi$ nontrivial!). It will turn out that these $L$-series each extend to meromorphic ⁷ functions on the plane with their own product formulae and functional equations. The proofs of these facts are similar to those in the case of the Zeta function, so we may not always be as careful and trust that arguments could be made more carefully. For example, we observe the following product formula

\[L(\chi,s)=\sum_{n\ge1}\frac{\chi(n)}{n^s}=\sum_{n\ge1}\prod_{p\mid n}\frac{\chi(p)^{v_p(n)}}{p^{v_p(n)s}}=\prod_p\sum_{n\ge0}\frac{\chi(p)^n}{p^{sn}}=\prod_p\parens{\frac1{1-\chi(p)p^{-s}}}\]

Before moving on, fix $\eps\in\bits$ such that $\chi(-1)=(-1)^{\eps}$. We call this $\eps$ the exponent of $\chi$. We use it to define the $\chi$-Gamma function

\[\Gamma(\chi, s)=\Gamma\parens{\frac{s+\eps}2}=\int_0^\infty e^{-t}t^{(s+\eps)/2}\frac{\d t}t.\]

Perhaps unsurprisingly, the next thing we do is perform a substitution ($t\mapsto\pi n^2u/N$) to get

\[\parens{\frac N\pi}^{\frac{s+\eps}2}\Gamma(\chi, s)n^{-s}=\int_0^\infty n^{\eps}e^{-\pi n^2u/N}u^{(s+\eps)/2}\frac{\d u}u.\]

Multiplying by $\chi(n)$ and summing over all $n\ge1$ gives

\[\parens{\frac N\pi}^{\frac{s+\eps}2}\Gamma(\chi, s)L(\chi, s)=\int_0^\infty u^{(s+\eps)/2}\sqbracks{\sum_{n=1}^\infty\chi(n)n^{\eps}e^{-\pi n^2u/N}}\frac{\d u}u.\]

Motivated by this, we also define a $\chi$-analogue of the theta series

\[\theta(\chi, s):=\sum_{n\in\Z}\chi(n)n^{\eps}e^{-\pi n^2s/N}\]

In the above definition, since $\chi$ is nontrivial, we have $\chi(0)=0$; hence, there is no $n=0$ term above. This may seem like a small remark, but the $n=0$ term in the case of trivial $\chi$ of conductor $N$ (i.e. in the case of Riemann zeta) was the source of the poles of the completed xi function. At this point, we would like to be able to apply Poisson summation ⁸ to get a functional equation for $\theta(\chi, z)$. To do this, first define

\[\theta_a(s):=\sum_{n\equiv a\pmod N}n^{\eps}e^{-\pi n^2s/N}=\sum_{k\in\Z}(Nk+a)^{\eps}e^{-\pi(Nk+a)^2s/N}\]

Next, we want to calculate the fourier transform of $f_a(x)=(Nx+a)^{\eps}e^{-\pi(Nx+a)^2s/N}$ ($\Re(s)>0$). For conveinence, let $g_0(x)=e^{-\pi x^2s/N}$ and $g_1(x)=xe^{-\pi x^2s/N}$. Then,

\[\begin{align*} \mc F(g_0)(\xi) &= \parens{\frac Ns}^{1/2}e^{-\pi\xi^2N/s}\\ \mc F(g_1)(\xi) &= \frac1{-2\pi i}\parens{\frac{\d}{\d\xi}\mc F(g_0)(\xi)} =-i\xi\parens{\frac Ns}^{3/2}e^{-\pi\xi^2N/s}\\ \mc F(f_a)(\xi) &= \mc F(g_{\eps}(Nx+a))(\xi) = e^{2\pi ia\xi/N}\mc F(g_{\eps}(Nx))(\xi) = \frac{e^{2\pi ia\xi/N}}N\mc F(g_{\eps})\parens{\frac\xi N}\\ &= \parens{\frac{-i\xi}s}^{\eps}(Ns)^{-1/2}e^{2\pi ia\xi/N}e^{-\pi\xi^2/(Ns)} \end{align*}\]

With that over, Poisson summation gives ⁹

\[\begin{align*} \theta_a(s)=\sum_{k\in\Z}f_a(k)=\sum_{k\in\Z}\mc F(f_a)(k) &=\sum_{k\in\Z}\parens{\frac{-ik}s}^{\eps}(Ns)^{-1/2}e^{2\pi iak/N}e^{-\pi k^2/(Ns)} \end{align*}\]

\[\begin{align*} \theta(\chi, s)=\sum_{n\in\Z}\chi(n)n^{\eps}e^{-\pi n^2s/N}=\sum_{a=0}^{N-1}\chi(a)\theta_a(s) &=\sum_{a=0}^{N-1}\sum_{k\in\Z}\chi(a)\parens{\frac{-ik}s}^{\eps}(Ns)^{-1/2}e^{2\pi iak/N}e^{-\pi k^2/(Ns)}\\ &=\sum_{k\in\Z}\sqbracks{\sum_{a=0}^{N-1}\chi(a)e^{2\pi iak/N}}\parens{\frac{-ik}s}^{\eps}\frac1{(Ns)^{1/2}}e^{-\pi k^2/(Ns)} \end{align*}.\]

The sum over $a$ above is a special kind of sum called a Gauss sum, which are sums of the form

\[\tau(\chi, k)=\sum_{a=0}^{N-1}\chi(a)e^{2\pi iak/N}.\]

Gauss sums enjoy the following list of properties (below, $\chi$ assumed primitive).

$\tau(\chi, k)=\conj\chi(k)\tau(\chi, 1)$ (the bar denotes complex conjugation).
$\abs{\tau(\chi)}=\sqrt N$.
$\tau(\conj\chi, 1)=\chi(-1)\conj{\tau(\chi, 1)}=(-1)^{\eps}\conj{\tau(\chi, 1)}$.

Exercise.

Now, let’s continue to simplify our expression for $\theta(\chi, s)$. Using the above (and that $-i=i^{-1}$) we see

\[\begin{align*} \theta(\chi, s) &=\sum_{n\in\Z}\chi(n)n^{\eps}e^{-\pi n^2s/N}\\ &=\sum_{k\in\Z}\tau(\chi, k)\parens{\frac{-ik}s}^{\eps}\frac1{(Ns)^{1/2}}e^{-\pi k^2/(Ns)}\\ &=\frac{\tau(\chi, 1)}{(is)^{\eps}{(Ns)^{1/2}}}\sum_{k\in\Z}{\conj\chi(k)k^{\eps}}e^{-\pi k^2/(Ns)}\\ &=\frac{\tau(\chi, 1)}{(is)^{\eps}(Ns)^{1/2}}\theta(\conj\chi, 1/s) \end{align*},\]

where I just did a bunch of algebra, so it’s very possible I made a mistake along the way, and the true expression should look slightly different ¹⁰. However, assuming this is not the case ¹¹, we have a nice functional equation for $\theta(\chi, s)$, so we can use this to give an analytic extension of $L(\chi, s)$ in much the same way as before. If you recall, we had shown previously that

\[\parens{\frac N\pi}^{\frac{s+\eps}2}\Gamma(\chi, s)L(\chi, s)=\int_0^\infty u^{(s+\eps)/2}\sqbracks{\sum_{n=1}^\infty\chi(n)n^{\eps}e^{-\pi n^2u/N}}\frac{\d u}u.\]

Hence, we will find a functional equation for the $\chi$-xi function ¹²

\[\xi(\chi, s)=\parens{\frac N\pi}^{\frac{s+\eps}2}\Gamma(\chi, s)L(\chi, s).\]

$\xi(\chi,s)$ extends to an entire function satisfying $$\xi(\chi, s) = W(\chi)\xi(\conj\chi, 1-s),$$ where $W(\chi)=\frac{\tau(\chi, 1)}{i^{\eps}\sqrt N}$.

First note that $\xi(\chi, s)=\frac12\int_0^\infty u^{(s+\eps)/2}{\theta(\chi, u)}\frac{\d u}u$, where there is no $``-1"$ there since $\chi(0)=0$. Since $\theta(\chi,u)=\frac{W(\chi)}{u^{1/2+\eps}}\theta(\bar\chi,1/u)$, we can calculate $$\begin{align*} \xi(\chi, s) &=\frac12\int_0^\infty u^{(s+\eps)/2}\theta(\chi, u)\frac{\d u}u\\ &=\frac12\int_0^1u^{(s+\eps)/2}\theta(\chi, u)\frac{\d u}u+\frac12\int_1^\infty u^{(s+\eps)/2}\theta(\chi,u)\frac{\d u}u\\ &=\frac{W(\chi)}2\int_0^1u^{(s-\eps-1)/2}\theta(\bar\chi,1/u)\frac{\d u}u + \frac12\int_1^\infty u^{(s+\eps)/2}\theta(\chi, u)\frac{\d u}u\\ &=\frac{W(\chi)}2\int_1^\infty u^{(1+\eps-s)/2}\theta(\bar\chi,u)\frac{\d u}u + \frac12\int_1^\infty u^{(s+\eps)/2}\theta(\chi, u)\frac{\d u}u\\ &=\frac12\int_1^\infty\sqbracks{W(\chi)u^{(1+\eps-s)/2}\theta(\bar\chi,u)+u^{(s+\eps)/2}\theta(\chi,u)}\frac{\d u}u . \end{align*}$$ Now, the integral above defines an entire function since $\theta(\chi, u)$ ($\chi$ fixed) decays rapidly, so $\xi(\chi, s)$ is entire. Note that $$W(\conj\chi)=\tau(\conj\chi,1)/(i^{\eps}\sqrt N)=(-1)^{\eps}\conj{\tau(\chi,1)}/(i^{\eps}\sqrt N)=\conj{\tau(\chi, 1)}/((-i)^{\eps}\sqrt N)=\conj{W(\chi)},$$ so $$\xi(\conj\chi, 1-s)=\frac12\int_1^\infty\sqbracks{\overline{W(\chi)}u^{(s+\eps)/2}\theta(\chi,u)+u^{(1-s+\eps)/2}\theta(\bar\chi,u)}\frac{\d u}u.$$ This formula looks pretty familiar, and indeed (after remarking that $\abs{W(\chi)}=1$) we see that $$\xi(\chi, s)=W(\chi)\xi(\conj\chi, 1-s).$$

$L(\chi, s)$ has an analytic continuation to the entire plane with no poles.

Just use $$L(\chi, s)=\parens{\frac\pi N}^{(s+\eps)/2}\frac{\xi(\chi, s)}{\Gamma(\chi, s)}.$$ Both $\xi(\chi,s)$ and $1/\Gamma(\chi,s)$ are entire, so the claim holds.

The same as the last corollary except without the implicit assumption that $\chi$ is primitive. To prove this, just notice that any character factors through a primitive one and then relate their $L$-functions.

Now that we’ve gotten this far, let’s return to the question of primes in arithmetic progressions. In order to prove Dirichlet’s theorem, we’ll need to make use of one non-trivial result that I will not prove in this post ¹³

For every non-trivial character (even the non-primitive ones) $\chi\in X(N)$, one has $L(\chi, 1)\neq0$.

Now, let

\[P_a:=\sum_{p\equiv a\pmod n}\frac1p,\]

and recall that

\[\mbf1_a(n) = \sum_{\chi\in X(N)}\frac{\chi(a)^{-1}}{\phi(N)}\chi(n).\]

Combined together, this gives

\[P_a=\sum_p\frac{\mbf1_a(p)}p=\sum_{\chi\in X(N)}\frac{\chi(a)^{-1}}{\phi(N)}\sum_p\frac{\chi(p)}p.\]

Now, note that (say, $s>1$)

\[\log L(\chi, s)=\prod_p\parens{\frac1{1-\chi(p)p^{-s}}}=\sum_p\frac{\chi(p)}{p^s}+\sum_p\sum_{n\ge2}\frac{\chi(p)^n}{np^{ns}}=\sum_p\frac{\chi(p)}{p^s}+O(1)\]

where I skipped a few steps because the argument is the same as when we showed $\sum_p\inv p=\infty$. Now, here’s the kicker: taking the limit as $s\to1^+$, we get

\[P_a=\sum_{p\equiv a\pmod n}\frac1p=\sum_{\chi\in X(N)}\frac{\chi(a)^{-1}}{\phi(N)}\log L(\chi, 1) + O(1) = \infty,\]

where the last equality comes from the fact that $\log L(\chi,1)=\infty$ iff $\chi$ is the trivial character! Thus, we’ve proven the following.

Fix some $a,N$ with $\gcd(a,N)=1$. Then, there are infinitely many primes $p$ such that $p\equiv a\pmod N$. Equivalently, the arithmetic progression $$\{\dots, a-2N, a-N, a, a+N, a+2N, \dots\}$$ contains infinitely many primes.

Dedekind

Dedekind’s name doesn’t appear in the title because I wasn’t originally going to talk about him, but he has a role in this story too. Unlike the previous two sections, this one will require some knowledge of basic algebraic number theory, and will not prove an infinitude result about primes ¹⁴.

We start by recalling some definitions/facts. A number field is a finite extension $K/\Q$. The integral closure of $\Z$ in $K$ is denoted $\ints K$, and is called $K$’s ring of integers. $\ints K$ is always a Dedekind domain (but not always a UFD), so any nonzero ideal in $\ints K$ factors into a unique product of prime ideals. Given an ideal $I\subseteq\ints K$, its norm is $N(I)=\abs{\ints K/I}$, the size of its residue ring.

Now, as it turns out, Dedekind’s favorite letter is the same as Riemann’s.

Given a number field $K/\Q$, the Dedekind $\zeta$-function is $$\zeta_K(s)=\sum_{I\subseteq\ints K}\frac1{N(I)^s},$$ where the sum is taken over all nonzero ideals of $K$. Note that $\zeta_{\Q}(s)=\zeta(s)$, the ordinary Riemann $\zeta$-function.

$\zeta_K(s)$ defines a holomorphic function in the half-plane $\Re(s)>1$. Perhaps unsurprisingly at this point, it is possible to show that $\zeta_K$ extends to a meromorphic function on the entire complex plane with a simple pole at $s=1$. This is harder to show than the analagous result for $\zeta(s),L(\chi, s)$ (although the idea is the same), so showing it is beyond the scope of this post.

One can use $\zeta_K$ to prove my earlier claim about the non-vanishing of $L$-functions attached to nontrivial characters at $s=1$ ¹⁵. This follows as a corollary of the following.

Let $K=\Q(\zeta_N)$ where $\zeta_N$ is a primitive $N$ root of unity. Then, $$\zeta_K(s)=\prod_{\chi\in X(N)}L(\chi, s).$$

The LHS above has a simple pole at $s=1$. The factor on the RHS belonging to the trivial character (which is just $\zeta(s)$ with some Euler factors removed) also has a simple pole at $s=1$. The rest of the factors on the RHS are holomorphic at $s=1$. Counting zeros/poles, we see that $L(\chi,1)\neq0$ if $\chi$ is nontrivial.

An analagous result holds for arbitrary abelian extensions of $\Q$. We’ll see a simple case of this.

First note that unique factorization of ideals gives a product formula

\[\zeta_K(s)=\prod_\mfp\frac1{1-N(\mfp)^{-s}}.\]

where $\mfp$ ranges over all (nonzero) prime ideals of $\ints K$. Now, fix a quadratic number field $K=\Q(\sqrt d)$ ($d\not\in\bits$ squarefree). Recall the splitting behavior of primes in $K$. Let ($k\in\Z$, and $p$ an odd prime)

\[\legendre kp=\begin{cases} 1&k\equiv x^2\pmod p\text{ for some }x\\ {-1}&k\not\equiv x^2\pmod p\text{ for all }x\\ 0&k\equiv0\pmod p \end{cases}\]

be the legendre symbol, and let $D=\disc(K/\Q)$ (i.e. $d$ if $d\equiv1\pmod4$ and $4d$ otherwise). Then, for an odd prime $p$, we have

\[\begin{cases} \text{$p$ is inert in $\ints K$}&\text{if }\legendre Dp=-1\\ \text{$p$ splits in $\ints K$}&\text{if }\legendre Dp=1\\ \text{$p$ is ramified in $\ints K$}&\text{if }\legendre Dp=0 \end{cases}\]

Because of this, we choose to extend the legendre symbol via

\[\begin{cases} \legendre D2=-1&\text{if $2$ is inert in $\ints K$}\\ \legendre D2=1&\text{if $2$ splits in $\ints K$}\\ \legendre D2=0&\text{if $2$ is ramified in $\ints K$} \end{cases}\]

We want to relate this splitting behavior to the Euler product for $\zeta_K(s)$. Consider an odd prime $p\in\Z$. If $p$ is inert, this it will contribute (since $p$ prime with norm $p^2$)

\[\frac1{1-p^{-2s}}=\frac1{1-p^{-s}}\frac1{1+p^{-s}}\]

to $\zeta_K(s)$. If $p$ splits, then it will contribute (since there are two primes above $p$, each with norm $p$)

\[\frac1{(1-p^{-s})^2}=\frac1{1-p^{-s}}\frac1{1-p^{-s}}\]

to $\zeta_K(s)$. Finally, if $p$ is ramified, then it will contribute (since there’s one prime over $p$ with norm $p$)

\[\frac1{1-p^{-s}}=\frac1{1-p^{-s}}\frac1{1-0p^{-s}}\]

to $\zeta_K(s)$. Thus, we see that

\[\zeta_K(s)=\prod_p\frac1{1-p^{-s}}\frac1{1-\legendre Dpp^{-s}}.\]

where the product is taken over rational primes $p\in\Z$. This looks like it is saying $\zeta_K(s)=\zeta(s)L(\legendre D\cdot,s)$, but is $\chi(n)=\legendre Dn$ even a Dirichlet character?

Yes, it is (since $D\equiv0,1\pmod4$). First, for $n=p_1^{e_1}\dots p_g^{e_g}$, we define

\[\chi(n)=\legendre Dn=\prod_{i=1}^g\legendre D{p_i}^{e_i},\]

so $\chi(n)$ is at least well-defined, if not a Dirichlet character. It is multiplicative by design, so to show that it is a Dirichlet character (mod $D$), we only need to know that $\chi(n)$ only depends on the value of $n\pmod D$. I must admit that I do not know how to show this ¹⁶, but taking its truth for granted for a bit, this gives $\zeta_K(s)=\zeta(s)L(\chi,s)$. If one takes $D=(-1)^{(q-1)/2}q$ for $q$ an odd prime, then there is only one quadratic Dirichlet character mod $D$ (i.e. one non-trivial homomorphism $U(D)\to{\pm1}$) since $\units{(\zmod q)}$ is cyclic. This character is $\chi(n)=\legendre nq$, but we’ve just shown that $\chi(n)=\legendre Dn$ is also a character. Thus,

\[\chi(p)=\legendre pq=\legendre Dp=\legendre{(-1)^{(q-1)/2}q}p=\legendre{-1}p^{(q-1)/2}\legendre qp=(-1)^{\frac{q-1}2\frac{p-1}2}\legendre qp,\]

which is the law of quadratic reciprocity. ¹⁷

The first time I saw this theorem, I thought it was the kind of dry, technical result that almost never shows up in the wild; I was wrong. ↩
You may object that expanding out the RHS let’s you pick a term with infinitely many prime factors, but this is a non-issue because those’ll all multiply out at 0, so we good. ↩
Actually, I have a guess. The theta function has terms that look like $e^{-s}$ while the zeta function has terms that look like $(1/n)^s$. If you want to exploit the theta function’s functional equation, then you need some kind of bridge between the two; this leads you to the Gamma function which has both a $e^{-\mrm{blah}}$ factor and a $\mrm{blah}^s$ factor. In fancier words, to introduce terms that help you relate the theta function to the zeta function you do something like take the Mellin transform of $s\mapsto e^{-\pi n^2s}$ (I say something like because I think we technically end up using the Mellin transform of $s\mapsto e^{-\pi n^2s^2}$ instead (and then substitute $u=x^2$), but potato potato) ↩
I think I’ve also seen this called the completed zeta function, but don’t quote me on that ↩
It’s a little known that this is something Dirichlet investigated to get his spirits up after failing to achieve his one, true goal: wiping out half of all life in the universe ↩
Really less a “dive” than a “dip our toes in the water” ↩
actually, holomorphic when the character is nontrivial ↩
See the end of my “Fourier Analysis” post if you don’t know what this is ↩
In hindsight, it would have been better to define $f(x) = (Nx)^{\eps}e^{-\pi(Nx)^2s/N}$, and then apply poisson summation to get $\sum_{k\in\Z}f(k+a) = \sum_{k\in\Z}F(f)(k)e^{2\pi ina}$
PS: –I really wish latex worked in these footnotes– (turns out dreams do come true) ↩
If you see a mistake somewhere, let me know ↩
At the very least, letting $N=1$ and $\chi=1$ (so $\eps=0$) recovers the functional equation for the classic theta function, as it should ↩
completed L function? ↩
Proving this is not too hard, but would take too much time. You can probably find a proof in like Davenport or something. ↩
But don’t worry, we will prove something involving primes. ↩
This is not the standard way to do so ↩
More accurately any proof I’ve seen of this uses quadratic reciprocity, and I don’t want to use that for reasons that will become apparent soon. ↩
I must admit, this whole section turned out more dubious than I intended. I wanted to present a (clean) proof of qudratic reciprocity, but it’s unclear to me how much machinary/grunt work one would need to turn this outline into a rigorous, non-circular proof ↩

Thoughts of a Programmer

Code, Math, Maybe some other stuff

Riemann, Dirichlet, and Their Favorite Letters

Riemann

Dirichlet

Shallow Dive

Back to Dirichlet

Dedekind