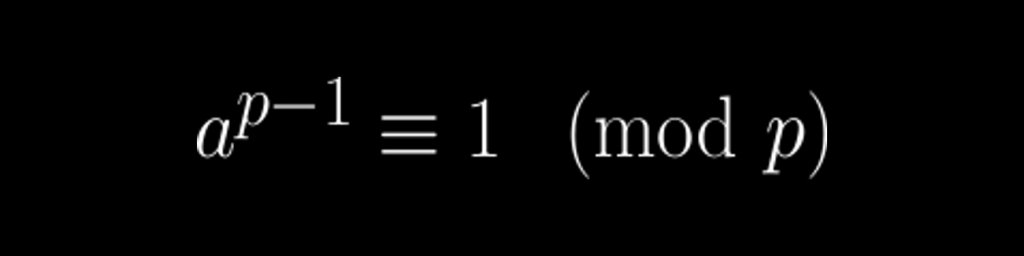I plan on writing a couple posts related to cryptography soon. Before I do that, I wanted to have a post covering some of the basics of modular arithmetic first, because this material will be needed for the cryptographic posts.

Divisibility

The first thing to know is that modular arithmetic is all about integers. We do not care about rationals, reals, or anything else, only integers ¹. As such, all our definitions have to be written in terms of integers, and the first such definition is that of divisibility. It is tempting to say that \(a\) divides \(b\) iff \(\frac ba\) is an integer, but writing \(\frac ba\) means we are entering the realm of rationals, which we cannot do. Therefore, we instead say that \(a\) divides \(b\) iff there exists an integer \(k\) such that \(b=ak\). This way we are defining divisibility in terms of multiplication (which is defined for integers) instead of division (which is not defined for integers in general). We write \(a|b\) when \(a\) divides \(b\). The following are a few properties of divisibility.

Mod

In the previous section I said that division was not defined for integers in general. That was a bit of a lie. It is, just not in the way we normally think of division.

Division algorithm:
For any two integers \(a\) and \(b\not=0\), there exists a unique pair of integers \(q\) and \(0\le{r}<|b|\) such that \(a=qb+r\). We call \(a\) the dividend, \(b\) the divisor \(q\) the quotient, and \(r\) the remainder.

From this theorem, we get the following definition.

Definition of \(a\bmod b\):
If \(a=qb+r\) where \(0\le{r}<|b|\), then we say that \(a\bmod b=r\).

In other words, \(a\bmod b\) is the remainder when \(a\) is divided by \(b\). Mod has some nice properties, such as
\(\begin{align*} [(a\bmod n)+(b\bmod n)]\bmod n&=(a+b)&\bmod n\\ (a\bmod n)(b\bmod n)\bmod n&=ab&\bmod n \end{align*}\)

These properties motivate the following definition.

Definition of \(a\equiv b\pmod n\):
We write \(a\equiv b\pmod n\) iff \((a-b)|n\). We read this as “\(a\) is congruent to \(b\) modulo \(n\)”.

Note that the above definition is equivalent to saying that \(a\equiv b\pmod n\) iff \(a\bmod n=b\bmod n\) ². It is easy to see that this new form of mod inherits some nice properties from the one we first introduced. Namely,

Finally, note that for all \(a\), there exits a \(b\) in \(\{0,1,2,\dots,n-1\}\) such that \(a\equiv b\pmod n\). This is because \(0\le{a}\bmod n<n\). This realization motivates the following definition.

Definition of \(\mathbb Z_n\):
\(\mathbb Z_n=\{a\in\mathbb Z:0\le{a}<|n|\}\) ³

Euclidean Algorithm

We begin this section with a definition or two.

A few definitions:
We call \(d\) the greatest common divisor of \(a\) and \(b\) if \(d|a\), \(d|b\), and no larger integer divdes both \(a\) and \(b\). We write \(\gcd(a,b)=d\) to denote that \(d\) is the greatest common divisor of \(a\) and \(b\).
We say that \(a\) and \(b\) are coprime (or relatively prime) if they have no common divisors other than \(1\). Equivalently, \(a\) and \(b\) are coprime iff \(\gcd(a,b)=1\).

We will see some of the uses of these concepts later in this post, but first, it would be nice if we had a way of calculating the greatest common divisior of two numbers. We could check each number that was less than them and find the largest one that divides both of them that way, but that would be time consuming. For a faster method, we use the Euclidean Algorithm.

The idea is to define a sequence of numbers \(r_0, r_1, r_2,\dots,r_n\) such that \(\gcd(a,b)=r_{n-1}\). To do this, we start with \(r_0=a\) and \(r_1=b\) where \(\mid a\mid\ge\mid b\mid\) ⁴. We then define subsequent \(r\)’s by division: \(r_{k-1} = qr_k + r_{k+1}\). In other words, \(r_{k+1}=r_{k-1}\bmod r_k\). We keep doing this until we finally reach \(r_n=0\). Our answer is then \(r_{n-1}\). This algorithm can be implemented in (python) code as follows:

def gcd(a,b):
	if abs(b) > abs(a):
		return gcd(abs(b),abs(a))
	elif b==0:
		return abs(a)
	else:
		return gcd(b,a%b)

To finish this section, let’s calculate the greatest common divisor of \(23456\) and \(123456\). \(\begin{matrix} 123456 &=& 5 &*& 23456 &+& &6176\\ 23456 &=& 3 &*& 6176 &+& &4928\\ 6176 &=& 1 &*& 4928 &+& &1248\\ 4928 &=& 3 &*& 1248 &+& &1184\\ 1248 &=& 1 &*& 1184 &+& &64\\ 1184 &=& 18 &*& 64 &+& &32\\ 64 &=& 2 &*& 32 &+& &0 \end{matrix}\)

Therefore, \(\gcd(123456,23456)=32\).

Analyzing the Euclidean Algorithm

This section will not be needed to understand the rest of this post and can be skipped. In it, we will discuss the Euclidean Algorithm slightly more formally, proving that it gives the correct answer and does so “quickly”.

Theorem 1:
For any \(a\) and \(b\), the Euclidean Algorithm terminates.

Pf: Let \(a\) and \(b\) be any integers ⁵ where, without loss of generality, \(\mid a\mid\ge\mid b\mid\). Then, we claim that the sequence of remainders in the Euclidean Algorithm – \(r_0=a,r_1=b,\dots,r_n\) – is finite. First, since \(r_{k+1}=r_{k-1}\bmod r_k\) for \(k\ge1\), we know that \(r_k\ge0\) for \(k\ge2\). Second, \(r_{k+1}\in\mathbb Z_{r_k}\), so \(\mid r_{k+1}\mid<\mid r_k\mid\). Therefore, the \(r_k\)’s form a strictly decreasing (in magnitude) sequence of integers greater than or equal to \(0\) for \(k\ge2\). Thus, there must be finitely many \(r_k\)’s. Else, the sequence would eventually be less than \(0\), a contradiction. \(\square\)

Theorem 2:
For any \(a\) and \(b\), the Euclidean Algorithm gives the correct value.

Pf: Let \(a\) and \(b\) be any integers, and let \(r_0,r_1,\dots,r_n\) be the sequence of remainders attained from the Euclidean Algorithm. Then, we claim that \(\gcd(a,b)=r_{n-1}\). To see this, first note that \(\gcd(0,n)=n\) for all \(n\) and so \(\gcd(r_{n-1},r_n)=\gcd(r_{n-1},0)=r_{n-1}\). We proceed to prove our claim by showing that \(\gcd(r_{k-1},r_k)=\gcd(r_k,r_{k+1})\) for all \(k\). Recall that \(r_{k-1} = qr_k + r_{k+1}\). Let \(d\) be any common divisor of \(r_{k-1}\) and \(r_k\). Then, \(d\) divides \(r_{k+1}=r_{k-1}-qr_k\), so \(d\) is a common divisor of \(r_k\) and \(r_{k+1}\). Similarily, if \(d'\) is a common divisor of \(r_k\) and \(r_{k+1}\), then \(d\) also divides \(r_{k-1}=qr_k+r_{k+1}\). As such, the common divisors of \(r_{k-1}\) and \(r_k\) are exactly the common divisors of \(r_k\) and \(r_{k+1}\). Namely, \(\gcd(r_{k-1}, r_k)=\gcd(r_k, r_{k+1})\). It follows by induction that \(r_{n-1}=\gcd(r_{n-1},r_n)=\gcd(r_0,r_1)=\gcd(a,b)\). \(\square\)

Lemma 1:
Given \(a\) and \(b\) where \(a\ge b\ge0\), let \(r_0=a,r_1=b,\dots,r_n\) be the sequence of remainders attained from the Euclidean Algorithm. Then, \(r_{k+2}\le\frac12r_k\) for all \(k\).

Pf: We proceed with a proof by contradiction. Suppose that for some \(k\), \(r_{k+2}>\frac12r_k\). Then, we have \(r_k\ge r_{k+1}>r_{k+2}>\frac12r_k\) and \(r_k=qr_{k+1}+r_{k+2}\). Since \(r_{k+1}>\frac12r_k\) and \(r_k\not=r_{k+2}\), we know that \(q=1\), so \(r_k=r_{k+1}+r_{k+2}\). However, since \(r_{k+1}>\frac12r_k\) and \(r_{k+2}>\frac12r_k\), \(r_k=r_{k+1}+r_{k+2}>\frac12r_k+\frac12r_k=r_k\), which is impossible. Therefore, there must not exist a \(k\) with \(r_{k+2}>\frac12r_k\). In other words, for all \(k\), \(r_{k+1}\le\frac12r_k\). \(\square\)

Theorem 3:
Given \(a\) and \(b\) where \(a\ge b\ge0\), let \(r_0=a,r_1=b,\dots,r_n\) be the sequence of remainders attained from the Euclidean Algorithm. Then, \(n\le2\log_2b + 3\).

Pf: Let \(m=2\lfloor\log_2b\rfloor+2=2(\lfloor\log_2b\rfloor+1)\) and note that, by the preceeding lemma, \(r_{1+2k}\le{r_1}/2^k\). Therefore, \(r_{1+m}\le r_1/2^{\lfloor\log_2b\rfloor+1}<1\). It follows from this that \(n\le1+m\le2\log_2b+3\). \(\square\)

Division \(\bmod n\)

One thing that may be surprising to hear is that modular arithmetic allows for division (sometimes). The division problem is as follows. Given \(a\) and \(n\), find a \(b\) such that \(ab\equiv1\pmod n\). We will simply take for granted the fact that such a \(b\) exits iff \(a\) and \(n\) are coprime and that such a \(b\) is unique (up to modular congruence) when it does exits. Furthermore, without going in to the details here, I will mention that \(b\) and be computed from \(a\) and \(n\) using the Extended Euclidean Algorithm or Fermat’s Little Theorem. If \(b\) exists, then we call it the inverse of \(a\pmod p\). Motivated by the fact that the inverse of \(a\) exists only when \(a\) is coprime to \(n\), we present the following definition.

Defintion of \(\mathbb Z_n^*\):
\(\mathbb Z_n^*\) is the set of all numbers less than or equal to \(n\) that are coprime to \(n\). This set is sometimes referred to as \(U(n)\).

Fermat’s Little Theorem

Fermat’s Little Theorem:
If \(p\) is a prime number, then for any integer \(a\) \(a^p\equiv a\pmod p\). Furthermore, if \(a\) is not divisible by \(p\), then \(a^{p-1}\equiv1\pmod p\).

This theorem is stated here without proof. The vigilent reader ⁶ will notice that if \(p\) is prime then all \(a\in\mathbb Z_p-\{0\}\) have an inverse \(\pmod p\) and that this inverse is \(b\equiv a^{p-2}\pmod p\).

Euler’s Totient Function

Euler’s Totient Function, also known as Euler’s phi Function, is a function \(\phi:\mathbb Z^+\rightarrow\mathbb Z^+\). \(\phi(n)\) is defined as the number of integers less than or equal to \(n\) that are coprime to \(n\). So, \(\phi(n)=|\mathbb Z_n^*|\). The following theorem’s involving Euler’s Totient Function are presented without proof.

Theorem 4:
If \(n=p^m\) for prime \(p\), then \(\phi(n)=p^{m-1}(p-1)\).

Theorem 5:
\(\phi(ab)=\phi(a)\phi(b)\) if \(a\) and \(b\) are coprime.

Theorem 6:
If \(a\) is coprime to \(b\), then \(a^{\phi(b)}\equiv1\pmod b\).