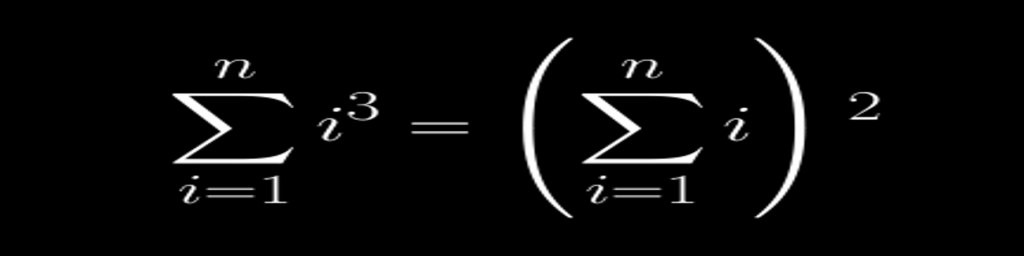Overview of Post

---

This post will be a quick derivation of the formulas for the sums of the first n numbers and the first n squares, followed by a more detailed derivation of the sum of the first n cubes.

\(\sum i\)

---

The trick here is to write each number twice. \(\begin{matrix} & 1 & + & 2 & + & 3 & + & \dots & + & n\\ + & n & + & (n-1) & + & (n-1) & + & \dots & + & 1\\ \hline & (n+1) & + & (n+1) & + & (n+1) & + & \dots & + & (n+1) \end{matrix}\)

Since there are \(n\) columns in the above addition, there are \(n\) copies of \((n+1)\) in the resulting sum. So, \(2\sum_{i=1}^ni=n(n+1)\). This gives us our final answer of

$$\begin{matrix} \sum\limits_{i=1}^ni=\frac{n(n+1)}2 \end{matrix}$$

\(\sum i^2\)

---

For this sum, I am just going to point to the derivation of it that is the best I have seen. This author explains it really nicely.

\(\sum i^3\)

---

For this sum, I am going to cheat a little. Most derivations of an explicit formula for this sum that I have seen use the fact that \(\sum_{i=1}^n i^4-(i-1)^4=n^4\) and then expand the summand of the left and do algebra until they end up with a solution. That method works, but I will use a different one that, unfortunately, asks a different question.

What is \((\sum_{i=1}^ni)^2\)?

From earlier in this post, we know that the answer is \((\sum_{i=1}^ni)^2=\left[\frac{n(n+1)}2\right]^2\), but can we come up with another formula? Let’s start by writing this product out explicitly:

$$(1+2+3+\dots+n)(1+2+3+\dots+n)$$

All of algebra is basically rewriting expressions, so let’s rewrite this expression. For each number \(k\) from \(1\) to \(n\), we will figure out its “coefficient” ¹ and then the expression will just be the sum of all the \(k\)’s multiplied by their coefficient. To keep things simple, \(k\)’s coefficient will be the sum of all the numbers less than or equal to \(k\) that it get’s multiplied by. As examples, \(1\)’s coefficient is \((1)\), \(2\)’s coefficient is \((1+2+1)\), and 3’s coefficient is \((1+2+3+2+1)\).

To figure out \(k\)’s coefficient in general, first consider the \(k\) on the left. It get’s multiplied by all the numbers from \(1\) to \(n\), so the numbers less than or equal to \(k\) that is get’s multplied by are just the numbers from \(1\) to \(k\). The same logic applies to the \(k\) on the right. So, the coefficient of \(k\) is \(2\sum_{i=0}^ki\)? Close. If you follow the logic closely, you will notice that we count \(k*k\) twice instead of one so the true coefficient of \(k\) is \(2(\sum_{i=0}^ki)-k\). Simplifying this expression yields \(2(\sum_{i=0}^ki)-k=k(k+1)-k=k^2\) as the coefficient of \(k\).

Now that we know each \(k\)’s coefficient, we can write

$$\left(\sum\limits_{i=1}^ni\right)^2=1(1^2)+2(2^2)+3(3^2)+\dots+n(n^2)=\sum\limits_{i=1}^ni^3$$

At this point, we could be done. We’ve answered our question, but our answer is very algebraic. It would be nice if we could have a visual way of explaining some of this math², so, with this hope in mind, we continue our investigation. Still considering the coefficient of \(k\), from our earlier discussion, it should not be to head to realize that \(k\)’s coefficient can be written as \(1+2+\dots+(k-1)+k+(k-1)+\dots+2+1\). This, as the picture below shows, is where we can begin to visualize. Thinking of each term in the sum as a diagonal in a square grid, it is easy to see that this sum is \(k^2\).

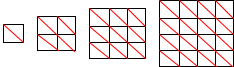
The nice part about having this visualization is that it does not require us knowing the sum of the first n numbers. The motivation for this invetigation was that we wanted to find an expression equal to the square of the sum of the first n numbers other than the explicit formula we already knew. If you already know an explicit formula for something, then it is hard to justify trying to find another (non-explicit) formula for it. However, even if we did not have an explicit formula, using this visual trick, we could still investigate this problem and gain a useful result (even if it does not give us an explicit formula). Finally, the following is the fruit of our efforts here:

$$\sum\limits_{i=1}^ni^3=\left(\sum\limits_{i=1}^ni\right)^2=\frac{n^2(n+1)^2}4$$

comments powered by Disqus