I have ideas for a couple posts I want to write, but unfortunately, they both will require some level of familiarity with abstract algebra, and I don’t want to just assume the reader has the necessary prereq and then go on writing them. Instead, I’ve given myself the ambitious ¹ goal of introducing most of the relevant algebra (spoiler: ²) in a series of blog posts beginning with this one on group theory.

Bit of a Disclaimer
I can’t possibly mention everything on a particular subject in one post, and I am not a particular fan of writing insanely long posts, so some things have to be cut. In particular, I aim to introduce most of the important topics in each subject without necessarily doing a deep dive, and while I will try to mention specific examples of things, I won’t spend too much time looking at them closely. It will be up to you to take the time to make sure the example makes sense. Because of this, I’ll try to include exercises that should be good checks of understanding. Finally, as always, things are presented according to my tastes and according to whatever order they happen to pop into my head; hence, they are not necessarily done the usual way.

What’s a group?

The natural place to start is with the definition of a group. Broadly speaking, groups follow two important themes in mathematics. These are the idea that, in math, we like to study collections of object that possess some kind of structure, and the idea that symmetry is often beneficial to doing mathematics. With that said, a group is intuitively a collection of symmetries ³ where you can think of a symmetry as some action ⁴ on an object that preserves it’s shape. We’ll see this more explicitly with our first example of a group.

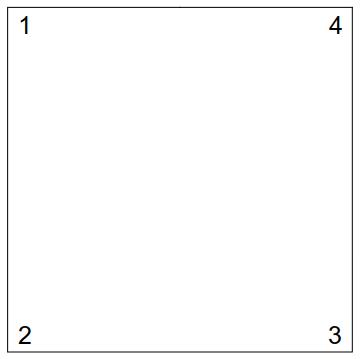
Before we get to a formal definition, let’s look at $D_8$, the group of symmetries of a square. These are all the actions you can perform on a square that leave it visually unchanged. To help make sense of what they are, we’ll visualize them using a square with labelled vertices.

Above is our square starting out. The simplest symmetry we can apply to it is the “do nothing” symmetry. However, that’s not a particularly exciting thing to do, so we spend a little more time thinking about how we can reposition the square, and decide to try rotating it 90 degrees (counterclockwise). After thinking about it some more, we realize we could also flip the square about it’s main diagonal (from 1 to 3)

Now the interesting thing happens when we try to compose these. What if we rotate and then flip (left image), or flip and then rotate (right image)?

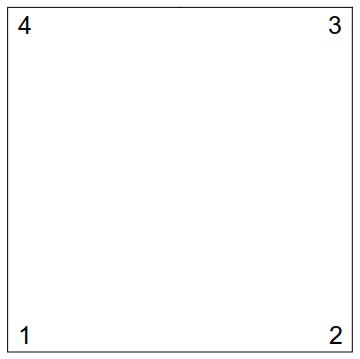
The first thing we notice is that these images are different, so order of symmetris matter. The second thing we may notice is that the image on the left is the previous right image (the flip) rotated 270 degrees, while the image on the right is the previous left image (the rotation) flipped across the other diagonal. Letting $R$ denote a $90\deg$ rotation, $F$ denote a flip across the main diagonal, and $F'$ denote a flip across the other diagonal, symbolically, we have

\[\begin{align*} FR = R^3F && RF = F'R \end{align*}\]

where $AB$ denote the result of first applying $B$ and then applying $A$. Now, there is more that can be said about this group, but I’ll leave the exploring to you.

From the above example, we can see some properties we might want in order to call something a collection of symmetries (i.e. a group). First, there should be a “do nothing” symmetry that just leaves things unchanged. Second, symmetries don’t necessarily have to commute (that is, $AB\neq BA$ in general), but should always be composable. I didn’t highlight these last two, but we should also expect that applying symmetries one after the other always gets you the same thing as long as you apply them in the same order (e.g. $A(BC)$ and $(AB)C$ should be the same), and we want to be able to undo an symmetry. Putting all these together, we get the following defintion.

Definition
A group $(G,\star)$ is a set $G$ together with an operation $\star:G\times G\rightarrow G$ satisfying the following for all $a,b,c\in G$
$\begin{align*} &\bullet a\star(b\star c)=(a\star b)\star c && \text{Associativity}\\ &\bullet \text{there exists an }e\in G\text{ such that }g\star e=g=e\star g\text{ for all }g\in G && \text{Identity}\\ &\bullet \text{there exists a }g\in G\text{ such that }g\star a=e=a\star g && \text{Inverses} \end{align*}$
If it turns out that additionally, $a\star b=b\star a$ for all $a,b\in G$, then $G$ is called an abelian group ⁵

That’s all there is to it. 3 simple conditions, and we’ll see that groups exhibit some well-behaved properties ⁶. Most of the time when talking about a specific group, the underlying operation will be understood, and so I’ll just refer to the group as $G$ instead of $(G,\star)$. Furthermore, the group operation is usually denoted $ab$ instead of $a\star b$ cause mathematicians are lazy. If the group is abelian, then $a+b$ is also common. Now that we have a definition, try to answer as many of these as you can.

Question
Are the following groups, abelian groups, or neither?

$D_8$

$(\Z,+)$

$(\Z,*)$

$(\R,+)$

$(\R,*)$

$(\R-\{0\},*)$

$(M_2(\R),+)$ the set of $2\times2$ matrices under addition

$(\Q-\{0\},*)$

$D_{2n}$ the set of symmetrices of a regular $n$-gon under composition

$(2\Z, +)$ the even numbers under addition

$(\Z_{12}, +)$ the integers mod 12 under addition

$(\Z_7-\{0\}, *)$ the integers mod 7 (except 0) under multiplication

the empty set under any operation you like

{e} the singleton consisting of only the identity

Basic Properties of Groups

Alright, now that we know what a group is, let’s see some of the benefits of studying them. The most obvious one is generality. If we show something is true for an arbitary group $G$, then we automatically know it’s true for the integers or the reals or matrices or what have you. So to start off, let’s prove some basic facts about groups.

Theorem
The identity element of a group is unique

Pf: Let $$G$$ be a group, and suppose that both $$e$$ and $$f$$ are identity elements. That is, for any $$a\in G$$, we have $$ae=a=ea$$ and $$af=a=fa$$. Hence, the theorem follows from
$$\begin{align*} e=ef=f \end{align*}$$ where we used the fact that $$f$$ is the identity on the left equality, and the fact that $$e$$ is the identity on the right equality. $$\square$$

The above theorem maybe isn’t too surprising. It basically says that there’s only one way to do nothing. The next theorem maybe also isn’t surprising either.

Theorem
Let $a\in G$ be an element of a group. Then, $a$ has a unique inverse.

Pf: Exercise for the reader

Now that we know that inverses are unique, we’ll denote the inverse of $a\in G$ by $a^{-1}$ (or $-a$ if $G$ is abelian). We’ll see a couple more proofs, and then we’ll get a look at something maybe a little less abstract.

Theorem (Socks and Shoes ⁷)
You put socks on before wearing shoes, but you have to remove your shoes before you can remove your socks. Symbollically, in a group $G$, for any $a,b\in G$, we have $(ab)^{-1}=b^{-1}a^{-1}$

Pf:
$$\begin{align*} (ab)(b^{-1}a^{-1}) &= a(bb^{-1})a^{-1}\\ &= aea^{-1}\\ &= aa{-1} \\ &= e \end{align*}$$
Since inverse are unique, we must have $$(ab)^{-1}=b^{-1}a^{-1}$$.$$\square$$

Theorem
If $(G,\star_G)$ and $(H,\star_H)$ are groups, then we can form the group $G\times H$ of pairs of elements of $G$ and $H$ with product $(g_1,h_1)(g_2,h_2)=(g_1\star_Gg_2,h_1\star_Hh_2)$

Pf: Exercise to the reader. Verify the group properties.

Note that the above group is called the direct product of $G$ and $H$. It is sometimes also denoted $G\oplus H$, and called their direct sum. These notions are the same here, but differ if you start talking about the direct product/sum of infinite collections of groups; however, we won’t get into that here.

Structure of Groups

Let’s return to our $D_8$ example. Recall that $R$ denotes rotation by 90 degrees and $F$ denotes a flip about the main diagonal. A fact that I will not prove here, but that you can spend some time convincing yourself of, is that $D_8$ is generated by $F$ and $D$ in the following sense.

Definition
Let $G$ be a group and $A\subset G$ be a subset of $G$. Then, we say $G$ is generated by $A$ if every elment of $G$ is some (finite) product of elements of $A$. Furthermore, if $A$ is finite ⁸, then we say that $G$ is finitely generated.

The remark about the definition amounts to saying that any symmetry of a square is really just the result of a bunch of flips and rotations. I mention this just out of curiousity. I had planned on using it as justification in giving a more explicity description for $D_8$, but unfortunately, the description would be longer than I’m willin to type out, so let’s look at a different group instead.

Out new star group is $\Z_4$ which is the integers under addition (mod 4). This group is special for a few reasons, but most of these are a result of it being generated by 1 element which motivates the following definition.

Definition
A group $G$ is called cyclic if it is generated by a single element. That is, it is cyclic there exists some $g\in G$ s.t. every $a\in G$ can be written in the form $g^n$ for some integer $n$.

In order to better understand $\Z_4$’s structure, we will look at its “multiplication” table.

\[\begin{array}{c | c | c | c} \Z_4 & 0 & 1 & 2 & 3 \\ \hline 0 & 0 & 1 & 2 & 3 \\ \hline 1 & 1 & 2 & 3 & 0 \\ \hline 2 & 2 & 3 & 0 & 1 \\ \hline 3 & 3 & 0 & 1 & 2 \\ \end{array}\]

Now, let’s consider the group $\Z_{10}^\times$. This is the integers (mod 10) that are coprime to 10 under multiplication. Hence, it’s multiplication table looks like

\[\begin{array}{c | c | c | c} \Z_{10}^\times & 1 & 3 & 7 & 9 \\ \hline 1 & 1 & 3 & 7 & 9 \\ \hline 3 & 3 & 9 & 1 & 7 \\ \hline 7 & 7 & 1 & 9 & 3 \\ \hline 9 & 9 & 7 & 3 & 1 \\ \end{array}\]

Now, you look at this and ask “what’s the point?” cause we’re just looking at some random tables. However, an important observation is that things like $\{0,1,2,3\}$ and $\{1,3,7,9\}$ are just symbols. It doesn’t really matter how we call the elemnts of the group; all that’s important is how they relate to each other. As an exercise in this way of thinking let’s relabel these tables using the following mappings

\[\begin{align*} &\Z_4 && \Z_{10}^\times\\ &0\mapsto a && 1\mapsto a\\ &1\mapsto b && 3\mapsto b\\ &2\mapsto c && 9\mapsto c\\ &3\mapsto d && 7\mapsto d \end{align*}\]

If we do that and remake the tables we will get the following for $\Z_4$

\[\begin{array}{ c | c | c | c} \Z_4 & a & b & c & d \\ \hline a & a & b & c & d \\ \hline b & b & c & d & a \\ \hline c & c & d & a & b \\ \hline d & d & a & b & c \\ \end{array}\]

Repeat this process for $\Z_{10}^\times$ and look at the table you get. If everything went as planned, you will see you ended up with exactly the same table. Since we said that the important thing was not the symbols but how they interacted with each other, this gives us complete justification in saying that, in some sense, $\Z_4$ and $\Z_{10}^\times$ are the same group. This is an idea we will now make rigorous via the notion of structure-preserving maps.

Definition
Let $(G,\star_G)$ and $(H,\star_H)$ be two groups. A homomorphism or group map $f:G\rightarrow H$ is a function with the property that for any $a,b\in G$, we have $f(a\star_Gb)=f(a)\star_Hf(b)$. If furthermore, $f$ is injective then we call it an embedding of $G$ into $H$, and it $f$ is bijective, then it is called an isomorphism and we say that $G$ and $H$ are isomorphic groups and denote this $G\simeq H$.

In essence, homomorphisms let us relate the structures of two groups by saying that they are doing something similar. If the homomorphism is injective, then it is essentially saying that a copy of $G$ lives inside of $H$. An example of this is the following

\[\begin{matrix} f:&\Z_3 &\longrightarrow& \Z_{15}\\ &a &\longmapsto& 5a \end{matrix}\]

It is not hard to verify that this is an injective homomorphism, so it lets us realize $\Z_3$ as sitting inside of $\Z_{15}$ in the form $f(\Z_3)=\{0,5,10\}$. By looking at their multiplication tables, we showed earlier that $\Z_4\simeq\Z_{10}^\times$. To get a better handle on homomorphims and see why they are the natural type of function to consider for groups, we’ll prove some quick theorems

Theorem
Let $f:G\rightarrow H$ be a homomorphism. Let $e_G,e_H$ be the identities of $G$ and $H$, respectively. Then, $f(e_G)=e_H$

Pf: Fix any $$g\in G$$ so $$f(g)=f(ge_G)=f(g)f(e_G)$$. If we multiply both sides (on the left) by $$f(g)^{-1}$$, then this equation becomes $$e_H=f(g)^{-1}f(g)=f(g)^{-1}f(g)f(e_G)=f(e_G)$$ $$\square$$

Theorem
Let $f:G\rightarrow H$ be a homomorphism. Then, for any $a\in G$ and $n\in\mathbb Z$, we have $f(a^n)=f(a)^n$.

Pf: We will show that $$f(a^{-1})=f(a)^{-1}$$ and the theorem will follow from an easy induction argument I won't bother doing. This case is an immediate consequence of $$f(a)f(a^{-1})=f(aa^{-1})=f(e_G)=e_H$$$$\square$$

Theorem
Let $G$ be a group and fix some $g\in G$. The function $f:G\rightarrow G$ defined by $f(x)=gx$ is a bijection, but not a homomorphism.

Pf: Exercise for the reader

Theorem
Let $f:G\rightarrow H$ be an isomorphism. Then, $f^{-1}:H\rightarrow G$ is also an isomorphism.

Pf: Exercise for the reader

Theorem
$\simeq$ is an equivalence relation on the class of groups.

Pf: Exercise for the reader

Subgroups

When introducing embeddings, I mentioned that they give us a way of viewing one group inside of another. This idea is formalized view the notion of subgroups which are pretty much exactly what they sound like.

Definition
Let $H\subseteq G$ be a subset of a group $G$. We say $H$ is a subgroup of $G$, denoted $H\le G$, if $H$ itself is a group.

Theorem
Let $f:G\rightarrow H$ be a homomorphism. Then, $f(G)\subseteq H$ is a subgroup of $H$. Furthermore, if $f$ is injective, then $f(G)\simeq G$.

Pf: Let $$I:=f(G)$$. To show that $$I$$ is a group, we need to show it contains the identity, has inverses, and it's multiplicatin is associative. Well, $$f(e_G)=e_H$$ and $$f(e_G)\in I$$ by definition, so we're good there. Furthermore, any element of $$I$$ can be written in the form of $$f(g)$$ for some $$g\in G$$. Hence, $$f(g^{-1})=f(g)^{-1}$$ is in $$I$$ as well, so we have inverses. Associativity follows from the fact that $$I$$'s multiplication is $$H$$'s multiplication, and it's associative. Finally, $$f\mid_I$$ is surjective by definition and so an isomorphism when $$f$$ is injective. $$\square$$

One thing worth mentioning is that while the definition of a subgroup requires that it first be a subset, we usually ignore this part and call any $H$ embaddable into $G$ a subgroup of $G$. Now that we have this notion of a subgroup, let’s see what we can do with it.

Theorem (2-step subgroup test)
Let $H\subseteq G$ be a non-empty subset of a group. Then, $H$ is a subgroup of $G$ if it is closed under multiplication, and contains inverses for each element.

Pf: Multiplication on $$H$$ inherits associativity from multiplication on $$G$$, and it has inverses by assumption. The group operation of $$H$$ is well-defined since it is closed, so the only thing to verify is that $$H$$ contains the identity. $$H$$ is non-empty so pick some $$h\in H$$. By assumption $$h^{-1}\in H$$ as well. Since $$H$$ is closed under multiplication, $$hh^{-1}\in H$$ so $$H$$ contains the identity. $$\square$$

Theorem (1-step subgroup test)
Let $H\subseteq G$ be a non-empty subset of $G$. Then, $H$ is a subgroup of $G$ if for all $a,b\in H$, we have $ab^{-1}\in H$ as well.

Pf: Exercise for the reader

Definition
Let $G$ be a group and fix some element $a\in G$. We say $\langle a\rangle=\{a^n:n\in\Z\}$ is the cyclic group generated by $a$.

Theorem
$\langle a\rangle\le G$

Pf: Pick any two elements, $a^n,a^m\in\gen a$. Then, $(a^n)(a^m)^{-1}=(a^n)(a^{-m})=a^{n-m}\in\gen a$. Furthermore, $\gen a$ is visibly non-empty, so it's a subgroup by the 1-step test. $\square$

So as an example, in $\Z$, $\langle3\rangle=3\Z$ the multiplies of $3$. This brings up a good source of confusion. When considering $\Z$ as a group under addition, $3^n$ is not $3$ raised to the $n$th power, but instead $3$ times $n$. Luckily, $\Z$ is abelian so this is normally written as $3n$, but just wanted to clarify.

One important notion in group theory, that unfortunately plays a minor role in this post, is that of the order of an element. For a group $G$, the order of the group is simply its size. For some element, $a\in G$ its order, denoted $|a|$ is the smallest positive exponent $n$ s.t. $a^n=e$. If no such $n$ exists, then $a$ is said to have infinite order. For a finite group, every element has some finite order (why?). Calling this the order of $a$ is justified by the following.

Exercise
$|a|=|\gen a|$

Note that a (finite) cyclic group is one where the order of some element is the order of the group. Furthermore, since I didn’t make this an exercise before, show that any cyclic group is abelian.

Definition
Let $f:G\rightarrow H$ be a group homomorphism. We define the kernel of $f$ as $\ker f=\{g\in G:f(g)=e\}$ the set of elements mapped to the identity.

Theorem
Let $f:G\rightarrow H$ be a group homomorphism. Then, $\ker f\le G$

Pf: Exercise for the reader

Since we now know some stuff about homormorphisms and subgroups, the majority of what follows will focus on proving two main theorems: Langrange’s Theorem and the First Isomorphism Theorem. After that, I will mention something that will be useful for one of the things I wanna talk about in a future post.

Cosets

The goal for this section is to find a way to generalize modular arithmetic to arbitrary groups. In modular arithmetic we can say things like $7\equiv4\pmod3$ when $(7-4)|3$, but if you generalize divison to groups in the obvious way, you don’t get anything useful; you’d end up with any two elements being equivalent as long as you modded out by something non-zero (why?). Because of this, instead of building off of division, we will follow the idea that modding out by $3$ is a way of treating $3$ as being $0$; this choice will manifest itself in an important placed on kernels.

Definition
Let $H\le G$ be a subgroup. We say that $H$ is normal if it is the kernel of some homomorphism. We denote this $H\trianglelefteq G$.

Returning to our $7\equiv4\pmod3$ example, from the perspective of $3$ being $0$ (i.e. $3\Z$ being normal), this equivalence is really expressing that $7=4+3\equiv4+0=4$. We can take this a step further by writing $7=1+2*3$ and $4=1+1*3$ which makes it apparent that they are equivalent because they are both $1$ more than a multiple of $3$. In the context of general groups, if we are going to treat some subgroup as being $0$, then any elements that are a fixed amount more than members of the subgroup should similarly be considered equivalent.

Definition
Let $H\le G$ be a subgroup, and fix some element $a\in G$. A (left) coset of $H$ is a set of the form $aH=\{ah:h\in H\}$

Exercise
Prove or disprove. For any subgroup $H\le G$ and element $a\in G$, we have that $aH=Ha$ where $Ha:=\{ha:h\in H\}$ is a right coset.

Hopefully you did the exercise. It turns out to be false in general, but miraculously, it is true for normal subgroups.

Theorem
Let $H\trianglelefteq G$ be a normal subgroup. Then, every left coset of $H$ is also a right coset (and vice versa).

Pf: Let $f:G\rightarrow K$ be a homomorphism with $\ker f=H$, and fix any $a\in G$. Then, an arbitrary element of $aH$ has the form $ah$ where $h\in H$. Note that $ah=aha^{-1}a$. To complete the proof we see that $f(aha^{-1})=f(a)f(h)f(a)^{-1}=f(a)ef(a)^{-1}=e$ so $aha^{-1}\in\ker f=H$ and so $ah=(aha^{-1})a\in Ha$. This shows that $aH\subseteq Ha$. The other direction can be shown analagously, so $aH=Ha$ for all $a$ which is more that sufficient to prove the claim. $$\square$$

The above theorem goes to show that normal subgroups are indeed special, and as it turns out, the converse of the theorem above is true as well ⁹, so this gives another way of characterizing normal subgroups. Now, recall that we want to come up with some notion of “modding out by a subgroup”, and so we want a way of saying when two elements of the big group are equivalent. We defined cosets with the idea that all of their members should be equivalent, and so the following shouldn’t be surprising.

Theorem
Let $H\le G$ be a (not necessarily normal) subgroup of $G$. Then, the relation $\sim$ defined by $x\sim y$ iff $xH=yH$ is an equivalence relation.

Pf: We need to show that $\sim$ is reflexive, symmetric, and transitive. It's obviously reflexive and symmetric, so we'll focus on transitivity. Suppose $x\sim y$ and $y\sim z$. Then, $xH=yH=zH$ so we have $x\sim z$, and we're done. $$\square$$

Corollary
The cosets of $H$ partition $G$

Now, we can prove our first major result of the post.

Theorem (Lagrange)
Let $H\le G$ be a subgroup. Then, $|H|$ divides $|G|$

Pf: Pick two cosets $aH$ and $bH$ of $G$. Then, the map $ah\mapsto (ba^{-1})ah$ is injective (result of every element having an inverse), and you get a similar injective map from $bH\rightarrow aH$. Thus, $|aH|=|bH|$ so all cosets have the same order (size). Since to cosets of $H$ partition $G$, assuming there are $k$ such cosets, we have $|G|=k|H|$. $$\square$$

Corollary
The order of an element of a group divides the order of the group.

Corollary
Every group of prime order is cyclic

Most everything after the definition of a coset wasn’t strictly needed for this, but is still good to know. We finally say what it means to mod out by a subgroup.

Definition
The index of $H$ in $G$ is the number of (left) cosets of $H$ in $G$ and is denoted $[G:H]$ or $|G:H|$.

Definition
Let $H\trianglelefteq G$ be a normal subgroup. We define the quotient group $G/H$ to be the set of left cosets of $H$ together with the multiplication operation $(aH)(bH)=(ab)H$.

When we mod a subgroup, we treat elements of the same coset as being equivalent, so instead of operating on individual elements, we operate on cosets instead. In practice, we can usally find a nice group that a quotient is isomorphic to, and so work with it instead of the quotient directly. This way, we can have quotients but still deal with elements instead of cosets. As a few examples

\[\begin{matrix} \frac{\Z\times\Z}{\Z\times\{e\}}\simeq\Z && \frac{\Z}{n\Z}\simeq\Z_n \end{matrix}\]

Now that we have this definied, we need to show that this is a good definition.

Theorem
Multiplication of the quotient group is well-defined. That is, if $xH=x'H$ and $yH=y'H$, then $(xy)H=(x'y')H$.

Pf: Suppose $$H\trianglelefteq G$$ and pick $$x,x',y,y'\in G$$ s.t. $$xH=x'H$$ and $$yH=y'H$$. Then, $$(xy)H=x(yH)=x(Hy)=(xH)y=(x'H)y=x'(Hy)=x'(Hy')=x'(y'H)=x'y'H$$. $\square$

The proof was short, but notice that we could only switch between left and right cosets so freely because we assumed that $H$ was normal. If $H$ is not normal, then this theorem is false. Now that we have well-definedness, the real crucial thing to show is up to you.

Theorem
Let $H\trianglelefteq G$. Then, $G/H$ is a group, and the quotient map $f:G\rightarrow G/H$ defined by $f(x)=x+H$ is a surjective homomorphism with $\ker f=H$.

Pf: (important) exercise to the reader.

Exercise
Prove that a subgroup $H\le G$ is normal iff $xH=Hx$ for all $x\in G$. After this, prove that this is the case iff $x^{-1}Hx\subseteq H$ for all $x\in G$.

Exercise
Prove that for an abelian group, every subgroup is normal.

Theorem
Let $H\trianglelefteq G$ be a normal group of finite index, and fix any $a\in G$. Then, $a^{[G:H]}\in H$.

Pf: Let $$f:G\rightarrow G/H$$ be the quotient map, and note that $$|G/H|=[G:H]$$. Thus, $$f(a)=a+H$$ has order dividing $$[G:H]$$ by Lagrange, so $$f(a^{[G:H]})=(a+H)^{[G:H]}=H$$ so $$a^{[G:H]}\in\ker f=H$$. $$\square$$

Diagrams et al.

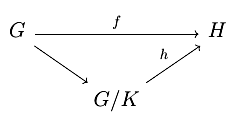
In this section, I’m gonna include some pictures, but they’ll be different from the type of images I usually include. Here, I’ll use so-called commutative diagrams. A diagram is a collection of objects (i.e. groups) with direct arrows (i.e. homomorphisms) drawn between them that makes it easier to discuss things when you have several functions going between different groups. We say such a diagram commutes when any path along arrows from one group to another gives the same result ¹⁰. This will make more sense when we see some.

I mentioned before that we would prove the first isomorphism theorem. Instead of proving it directly, we will derive it as a corollary of a better theorem in my opinion.

Factor Theorem
Let $f:G\rightarrow H$ be a homomorphism, and let $K\le\ker f$. Then, there exists a unique homomorphism $h:G/K\rightarrow H$ such that $f$ factors through $h$ in the sense that the following diagram commutes
That is, $f$ is the composition of $h$ and the quotient map. Furthermore, $h$ is injective iff $K=\ker f$, and $h$ is surjective iff $f$ is surjective.

Pf: Let $$f,G,H,K$$ be as in the statement of the theorem. We first want to show that there is a unique $$h:G/K\rightarrow H$$ such that $$h(xK)=f(x)$$ for all $$x\in G$$. Well, define $$h$$ based solely off of this equation. Every element of $$G/K$$ is of the form $$xK$$ and $$f(x)$$ is unique given a choice of $$x$$, so this gives a unique satisying $$h$$. We now need to make sure that $$h$$ is well-definied (the fact that it's a homomorphism follows from $$f$$ being one), so pick $$g,g'\in G$$ s.t. $$gK=g'K$$. Then, $$g^{-1}g'\in K$$ so $$f(g')=f(gg^{-1}g')=f(g)f(g^{-1}g')=f(g)\implies h(gK)=h(g'K)$$ so we're good. For the statements about injectivity and surjectivity, convince yourself that a homomorphism is injective iff it's kernel is trivial, and that $$\image(h)=\image(f)$$. $$\square$$

Corollary (First isomorphism theorem)
Let $f:G\rightarrow H$ be a surjective homomorphism. Then, $G/\ker f\simeq H$.

Pf: By the above theorem, $$f$$ must factor through some map $$g:G/\ker f\rightarrow H$$. Furthermore, this map must be injective and surjective since we're factoring through the full kernel and $$f$$ was surjective. Thus, we have an isomorphism. $$\square$$

Lagrange’s Theorem and the first isomorphism theorem are two of the big, foundational theorems for group theory, and we’ve now proven both of them. Normally, this would be a good place to stop, but there’s one last thing I want to quickly introduce ¹¹.

Definition
Consider a sequence of groups and homomorphisms between them
$$\begin{CD} G_1 @>f_1>> G_2 @>f_2>> G_3 @>f_3>> G_4 @>f_4>> \dots @>f_{n-1}>> G_n \end{CD}$$ We say such a sequence is exact if $\image(f_k)=\ker(f_{k+1})$ for all $1\le k<n$. In particular, a short exact sequence is an exact sequence of the form $$\begin{CD} \{e\} @>>> N @>f>> G @>g>> H @>>> \{e\} \end{CD}$$ where $\{e\}$ is the trivial group.

The first time I saw exact sequences, all I could think was, “Why? Who cares?” At first glance, they seem pretty artificial, but they actually give a compact way of codifying some information about how groups are related to each other. Let’s look at the short exact sequence appearing in the above definition for example. The fact that the sequence is exact that $N$ says that the image of the incoming map (which must send the trivial element to the identity in $N$) is the kernal of $f$. This is just the statement that $\ker f=\{e\}$ or equivalently that $f$ is injective! Similarly, exactness at $H$ says that the image of $g$ is the kernel of the map sending all of $H$ to the identity, so $\image g=H$ and $g$ is surjective! Finally, exactness at $G$ says that $\image f=\ker g$. Since we know $f$ is injective, this means we can embed $N$ in $G$ as a normal subgroup. Furthermore, since $g$ is surjective, the first isomorphism theorem tells us that $G/N\simeq G/\image f\simeq G/\ker g\simeq H$, so we get the sense that $G$ is somehow made up from $N$ and $H$ (the simplest example is $G\simeq N\times H$, and you can easily pick $f,g$ to form a short exact sequence in this case, but other choices of $G$ may work too). Because of this observation, we make our final definition.

Definition
We say $G$ is an extension of $N$ by $H$ ¹² if there exists a short exact sequence
$$\begin{CD} \{e\} @>>> N @>f>> G @>g>> H @>>> \{e\} \end{CD}$$

ambitious because historically speaking I’m bad at sticking with these kinds of things ↩
I imagine one post of group theory, one on rings/fields, and then one on noetherian rings and dedekind domains ↩
whatever that means ↩
you won’t see this much here, but it’s important to keep in mind that groups often do perform some action on an object, and studying these group actions can lead to good math. ↩
not in this algebra sequence, but at some point I hope to give reason to why this isn’t the most appropriate name, and these things should really be called Z-modules instead ↩
not in this algebra sequence, but at some point I hope to give reason to why actually groups in general are really ugly and do some pathological things ↩
Socks and Sandals if you prefer ↩
This is not quite the definition of finitely generated, but works in almost all (actually, maybe all. I don’t know of a counterexample) cases ↩
This might be more apparent after we define quotient groups ↩
Basically every diagram you see in the wild will be commutative ↩
Before I forget to mention this, exercise: look up the like 3 other isomorphism theorems. Also, there’s a decent amount of group theory you’d usually learn leading up to some of the stuff I’ve mentioned here that I didn’t bring up at all. ↩
Some people say G is an extension of H by N instead. Doesn’t really matter ↩

Thoughts of a Programmer

Code, Math, Maybe some other stuff

Algebra Part I

What’s a group?

Basic Properties of Groups

Structure of Groups

Subgroups

Cosets

Diagrams et al.