Spectral Sequences

Back when I was in high-school, I became really interested in this thing called “machine learning.” The main idea is that you bombard some algorithm with a ton of examples (of a task being performed or of objects being classified), and then you cross your fingers and hope it has managed to reliably learn how to do what the examples showcased. One big draw of this approach is that there are many tasks where it is not clear how to accomplish them, but where it feels like there has to be enough information present that accomplishing them is possible. For example, imagine writing a program that takes in an image and tells you if there’s a bird in it; this is hard to do algorithmically, but certainly the pixel values of an image contain enough information to decide whether or not there’s a bird there 1. The moral of this detour is that sometimes we find ourselves in situations where we have lots of information available to tackle some problem, but figuring out how to utilize all that information is quite tricky. Imagine, for example, you have some topological space $X$ with a filtration $ \newcommand{\msC}{\ms C} \newcommand{\msA}{\ms A} \DeclareMathOperator{\Ch}{Ch} \DeclareMathOperator{\CoCh}{CoCh} \DeclareMathOperator{\Fil}{Fil} \DeclareMathOperator{\Tot}{Tot} $

\[X^0\subseteq X^1\subseteq X^2\subseteq\cdots\subseteq X\]

such that $X=\dirlim X^k$. The example to keep in mind is $X$ a CW-complex, and $X^k$ its $k$-skeleton. Intuitively, the cohomology groups $\hom^n(X^k)$ should approximate $\hom^n(X)$, so if you know all of them, then you should have enough information to say something about $\hom^n(X)$. Figuring out exactly what you can say in this situation (and others) is the aim of spectral sequences, which, if you haven’t guessed yet, are the stars of this post.

Specifically, I’ll speak abstractly about two common sources of spectral sequence 2. Because I really wanna talk about this material 3, I won’t do my usual thing of trying to write as if everything I’ve written previously on this blog forms a dense subset of what I’m assume the reader knows. Instead, I’ll assume you’re comfortable with the words like cohomology, category, and other things that start with a c, then go from there. With that said, I’ll briefly define abelian categories, say what a spectral sequence is, given an example, and depending on how I’m feeling at the end, either say the word hypercohomology or save that for a future post. Let’s get started$\dots$ 4

Abelian Categories Briefly

An abelian category is one that behaves like the category of abelian groups. These form the main setting for much of homological algebra, so it’s probably worthwhile to see how they’re defined at least once. I’ll build up the definition piece by piece.

A category $\msC$ is called preadditive if every hom set $\Hom_{\msC}(A,B)$ (where $A,B\in\ob\msC$) is an abelian group such that composition of morphisms is bilinear.

To get to the next step, we need the notion of a biproduct, which is just an object that is both a product (think direct product) and coproduct (think direct sum). I guess I’ll define what a coproduct (of two objects) is, and leave defining product to you.

Let $\msC$ be a category, and fix objects $X_1,X_2\in\ob\ms C$. A coproduct of $X_1$ and $X_2$ is an object $X$ (often denoted $X_1\amalg X_2$) together with a pair of morphisms $\iota_1:X_1\to X,\iota_2:X_2\to X$ satisfying the below universal property:
  • for every object $Y\in\msC$ with maps $f_1:X_1\to Y$ and $f_2:X_2\to Y$, there exists a unique morphism $f:X\to Y$ such that the below diagram commutes
In short, it's an object such that "maps out of the coproduct are maps out of each factor." In medium, it is an object that is initial in the category of objects of $\msC$ with maps from $X_1$ and $X_2$.
The above defines a binary coproduct. You can easily extend this definition to that of a coproduct of objects $X_i$ where $i\in I$ ranges through an arbitrary index set.
Coproducts in $\textrm{Set}$ are disjoint unions, and coproducts in $\textrm{Ab}$ are direct sums.

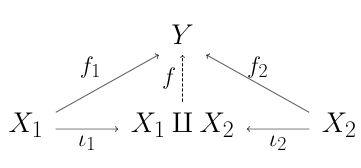
Now, define products in a dual way, i.e. “maps into products are maps into each factor,” and then say a biproduct is an object that is both a product and coproduct (of the same set of objects). This brings us to

A preadditive category $\msC$ is called additive if every finite set of objects has a biproduct, and a zero object $0\in\msC$ (i.e. one that is both initial and final) exists.
Given $A,B\in\msC$, an additive category, let $0_{AB}\in\Hom_{\msC}(A,B)$ denote the morphism given composed from $A\to0\to B$.

For the next step, we need to know how to define kernels and cokernels.

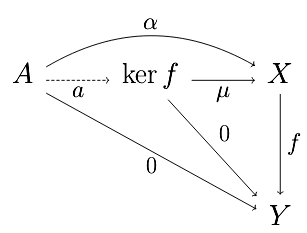
Let $\msC$ be an additive category (or even just a category with zero morphisms), and fix any morphism $f:X\to Y$ in $\msC$. Then, an object $M$ is called a kernel of $f$, usually denoted $\ker f$, if it is final in the category of maps to $A$ "killed by $f$". I mean to say, there exists a morphism $\mu:M\to X$ such that for any morphism $\alpha:A\to X$ such that $f\circ\alpha=0_{AY}$, there exists a unique $a:A\to M$ making the following diagram commutes

Cokernels are define similarly as being initial with respect to maps $\nu:Y\to N$ such that $\nu\circ f=0$. Now,

An additive category is preabelian if every morphism has both a kernel and a cokernel.

Almost there. Note that if $\mu:\ker f\to X$ is the kernel of a map $f:X\to Y$, then $\mu$ is a monomorphism, i.e. if we have $a:A\to\ker f$ and $b:A\to\ker f$ such that $\mu\circ a=\mu\circ b$, then $a=b$ 5. We would like every monomorphism to arise in this way. Similarly, cokernels are epimorphisms, and we would like them to be the only epimorphisms 6.

Let $\msC$ be a preabelian category. A monomorphism is called normal if it is also a kernel, and an epimorphism is called conormal (or still just normal) if it is also a cokernel.
A preabelian category is an abelian category if every monomorphism is normal and every epimorphism is conormal.

To sum it all up, an abelian category is one with a zero object, all binary biproducts, all kernels and cokernels, and where all monomorphisms/epimorphisms are normal. Lot’s of the language used in the theory of abelian groups (quotients, subobjects, exactness, etc.) carries over to arbitrary abelian categories in a fairly straightforward manner, so you can often get away with imagining elements of abstract abelian categories as just being abelian groups or $R$-modules, or what have you. Before moving on, here’s one important example of an abelian category.

Fix an additive category $\msA$. A chain complex 7 $A_\bullet$ is a sequence

\[A_\bullet:\cdots\too A_1\xtoo{d_1} A_0\xtoo{d_0} A_{-1}\too\cdots\]

of morphisms in $\msA$ such that $d_n\circ d_{n+1}=0$ for all $n$. A chain map $f:A_\bullet\to B_\bullet$ is a commutative diagram

\[\begin{CD} \cdots @>>> A_1 @>d_1>> A_0 @>d_0>> A_{-1} @>>> \cdots\\ &@Vf_{-1}VV @Vf_0VV @Vf_1VV\\ \cdots @>>> B_1 @>d_1>> B_0 @>d_0>> B_{-1} @>>> \cdots \end{CD}\]

whose rows are chain complexes. Let $\Ch_\bullet(\msA)$ denote the category whose objects are chain complexes in $\msA$, and whose morphisms are chain maps.

Show that $\Ch_\bullet(\msA)$ is an abelian category if $\msA$ is (hint: do everything componentwise).

Before going on, I should maybe also say what homology is.

Given a category $\msC$ and a morphism $f:X\to Y$ in $\msC$, the image of $f$ is an object $I$, usually denoted $\im f$, with a monomorphism $\iota:I\to Y$ that is initial among morphisms that $f$ factors through. That is, there exists a morphism $e:X\to I$ such that for any morphisms $e':X\to I'$ and $m':I'\to Y$ where $f=m'\circ e'$, there is a unique morphism $v:I\to I'$ making the below diagram commute
When $\msC$ is an abelian category, we have $\im f\simeq\ker(\coker f)$.
Let $A_\bullet=\bracks{d_n:A_n\to A_{n-1}}$ be a chain complex. Its $n$th homology object should intuitively be $\hom_n(A_\bullet)=\ker d_n/\im d_{n+1}$. I guess the way we make this formal/general/whatever is by setting $$\hom_n(A_\bullet):=\coker\parens{\im d_{n+1}\to\ker d_n}$$ where the map $\im d_{n+1}\to\ker d_n$ exists (and is unique) because the composition $\im d_{n+1}\to A_n\xto{d_n}A_{n+1}$ is the zero map.

Spectral Sequence of a Filtered Complex

Now we start developing the good stuff. I should probably start by saying that I will only be considering spectral sequences in cohomology in this post, so, for example, we’ll we be working in the (abelian) category $\CoCh(\msA)$ of cochain complexes of an abelian category $\msA$. 8

For the remainder of this section, fix some abelian category $\msA$. Probably a good place to start here is with the definition of a filtered complex.

A decreasing filtration $F$ on an object $A\in\msA$ is a famility $(F^nA)_{n\in\Z}$ of subobjects of $A$ such that $$A\supseteq\dots\supseteq F^nA\supseteq F^{n+1}A\supseteq\dots\supseteq0.$$ A filtered object of $\msA$ is a pair $(A,F)$ consisting of an object $A\in\msA$ and a decreasing filtration $F$ on $A$. A morphism $(A_1,F_1)\to(A_2,F_2)$ of filtered objects is a morphism $\phi:A_1\to A_2$ such that $\phi(F_1^kA_1)\subset F^k_2A_2$ for all $k\in\Z$. We thus arrive at the category $\Fil(\msA)$ of filtered objects.
Given a filtered object $(A,F)$, we get associated graded objects $G^kA=F^kA/F^{k+1}A$.
A filtration $F$ on an object $A$ is called bounded (or finite) if there exists $n,m$ such that $F^nA=A$ and $F^mA=0$.
A filtered cochain complex is an object in the category $\CoCh(\Fil(\msA))$ (equivalently, one in $\Fil(\CoCh(\msA))$).

Let $A^\bullet=\bracks{d_n:A^n\to A^{n+1}}$ be a filtered cochain complex. Its differential $d$ induces a well-defined differential $G^pA^n\to G^pA^{n+1}$, so we get an associated graded chain complex $G^pA^\bullet$. Furthermore, we get a natural filtration on cohomology given by

\[F^p\hom^n(A^\bullet)=\bracks{\alpha\in\hom^n(A^\bullet)\mid\exists x\in F^pA^n:\alpha=[x]},\]

which has assocated graded pieces $G^p\hom^n(A^\bullet)$. If we’re lucky this grading will actually determine the cohomology of $A^\bullet$ via the short exact sequences

\[0\too F^{p+1}\pull\hom(A^\bullet)\too F^p\pull\hom(A^\bullet)\too G^p\pull\hom(A^\bullet)\too0.\]

It’s sometimes easier to compute $\pull\hom(G^pA^\bullet)$ than $G^p\pull\hom(A^\bullet)$, so we may wonder about comparing the two in order to eventual get a handle on $\pull\hom(A^\bullet)$. It turns out that we can get from one to the other via a series of “successive approximations.”

We start by denoting the associated graded complex by

\[E_0^{p,q}:=G^pA^{p+q}\text{ }\text{ with differential }\text{ }d_0^{p,q}:E^{p,q}_ 0\to E_0^{p,q+1}.\]

Denote the cohomology of this complex by

\[E_1^{p,q}:=\hom^{p+q}(G^pA^\bullet)=\frac{\ker\big({d_0^{p,q}:E_0^{p,q}\to E_0^{p,q+1}}\big)}{\im\parens{d_0^{p,q-1}:E_0^{p,q-1}\to E_0^{p,q}}}=\frac{\ker\big({d_0^{p,q}:G^pA^{p+q}\to G^pA^{p+q+1}}\big)}{\im\parens{d_0^{p,q-1}:G^pA^{p+q-1}\to G^pA^{p+q}}},\]

which we think of as a “first-order approximation” to $\pull\hom(A^\bullet)$. Let’s explicitly construct a second-order approximation. Note that a cohomology class $\alpha\in E_1^{p,q}$ can be represented by a chain $x\in F^pA^{p+q}$ with differential $dx\in F^{p+1}A^{p+q+1}$. With this in mind, we define

\[\mapdesc{d_1^{p,q}}{E_1^{p,q}}{E_1^{p+1,q}}{\alpha}{[dx]}\]

One easily sees that $d_1^{p,q}\circ d_1^{p+1,q}=0$ 9, and so we are justified in defining

\[E_2^{p,q}:=\hom^p(E_1^{\bullet, q})=\frac{\ker\big({d_1^{p,q}:E_1^{p,q}\to E_1^{p+1,q}\big)}}{\im\parens{d_1^{p-1,q}:E_1^{p-1,q}\to E_1^{p,q}}}.\]

As a sanity check to make sure things make sense, try doing the following.

Suppose that $F^{-1}A^\bullet=0$ and $F^1A^\bullet=A^\bullet$ (so $F^0A^\bullet$ is just some subcomplex). Show that in this case, we have $E_2^{p,q}=G^p\hom^{p+q}(A^\bullet)$.

Returning to general filtrations, we can continue to construct higher order approximations. Doing one more step before handling general approximations, note that an $\alpha\in E_2^{p,q}$ can be represented by some $\st\alpha\in E_1^{p,q}$ with differential $d_1\st\alpha=0\in E_1^{p+1,q}$. Since $d_1\st\alpha=[dx]$ where $x\in F^pA^{p+q}$ is any chain representing $\alpha$, we can take $dx$ to be the zero element of $\ker(d_0^{p+1,q})$, which is to say we can take $x$ s.t. $dx\in F^{p+2}A^{p+q+1}$ 10. This suggest we can get a map $d_2^{p,q}:E_2^{p,q}\to E_2^{p+2,q-1}$.

Based on what we’ve seen so far, it seems as though elements of an $r$th order approximation $E_r^{p,q}$ should be ultimately represented by cycles $x\in F^pA^{p+q}$ such that $dx\in F^{p+r}A^{p+q+1}$. This turns out to be exactly the case. For $r\ge0$, define

\[\begin{align*} Z_r^{p,q} &=\frac{F^pA^{p+q}\cap\inv d\parens{F^{p+r}A^{p+q+1}}+F^{p+1}A^{p+q}}{F^{p+1}A^{p+q}}\\ B_r^{p,q} &=\frac{F^pA^{p+q}\cap d\parens{F^{p-r+1}A^{p+q-1}}+F^{p+1}A^{p+q}}{F^{p+1}A^{p+q}} \end{align*}\]

and let $E_r^{p,q}=Z_r^{p,q}/B_r^{p,q}$. On these objects, we can define a differential

\[\mapdesc{d_r^{p,q}}{E_r^{p,q}}{E_r^{p+r,q-r+1}}{[z]}{[dz]}\]

where $z\in F^pA^{p+q}\cap\inv d(F^{p+r}A^{p+q+1})$. Note that $d_r$ has bidegree $(r,1-r)$. With these definitions set up, we have the following 11.

  1. The map $d_r^{p,q}$ is well-defined with $d_r^{p,q}\circ d_r^{p-r,q+r-1}=0$.
  2. $E_{r+1}$ is given by taking the cohomology of $E_r$, i.e. $$E_{r+1}^{p,q}\simeq\frac{\ker\parens{d_r^{p,q}:E_r^{p,q}\to E_r^{p+r,q-r+1}}}{\im\parens{d_r^{p-r,q+r-1}:E_r^{p-r,q+r-1}\to E_r^{p,q}}}$$
  3. $E_1^{p,q}=\hom^{p+q}(G^pA^\bullet)$.
  4. If the filtration of $A^\bullet$ is bounded, then for every $p,q$, for $r$ sufficiently large, we have $E_r^{p,q}=G^p\hom^{p+q}(A^\bullet)$. In this case, we say $E_1$ converges (or abuts) to $\hom^{p+q}(A^\bullet)$, and denote this $E_1^{p,q}\implies\hom^{p+q}(A^\bullet)$.
For convenience, let $K_r^{p,q}=F^pA^{p+q}\cap\inv d(F^{p+r}A^{p+q+1})$ and $I_r^{p,q}=F^pA^{p+q}\cap d(F^{p-r+1}A^{p+q-1})$.
  1. It's clear by definitions that every element of $E_r^{p,q}$ can be represented by some $z\in K_r^{p,q}$ just by definition. Given such a $z$, we have $dz\in K_r^{p+r,q-r+1}$ because $dz\in F^{p+r}A^{p+q+1}$ and $d^2z=0$. Hence, it remains to show that if $z\in I_r^{p,q}$, then $dz\in I_r^{p+r,q-r+1}$. Well, if $z\in I_r^{p,q}$, then $z=dw$ with $w\in F^{p-r+1}A^{p+q-1}$, so $dz=d^2w=0\in F^{p+r}A^{p+q+1}$. Hence, $dz\in I_r^{p+r,q-r+1}$ as desired. It's clear that $d_r^2=0$ since $d^2=0$.
  2. Note that $K_{r+1}^{p,q}\subset K_r^{p,q}$, so there's a natual induced injection $Z_{r+1}^{p,q}\into Z_r^{p,q}$. Composing this with the quotient map gives a map $\phi:Z_{r+1}^{p,q}\to E_r^{p,q}$. Now, for $z\in K_{r+1}^{p,q}$, we have $\phi([z])\in\ker d_r^{p,q}$ since $d_r(\phi([z]))=[dz]\in E_r^{p+r,q-r+1}$ and $dz\in F^{p+r+1}A^{p+q+1}=F^{(p+r)+1}A^{(p+r)+(q-r+1)}$. In fact, we have that $\phi$ surjects onto $\ker d_r^{p,q}$ because its image, by definition, contains every $z$ s.t. $dz\in F^{p+r+1}A^{p+q+1}$. Now, we claim that $\ker\phi=B_r^{p,q}$ which suffices to prove 2. It's clear that $I_{r+1}^{p,q}\subset I_r^{p,q}$, so $B_r^{p,q}\subset\ker\phi$. Conversely, suppose that $z\in\ker\phi\subset Z_{r+1}^{p,q}$. Well, $\phi(z)=[z]$, so this means that $z\in B_r^{p,q}$. Hence, $z\in B_r^{p,q}\cap Z_{r+1}^{p,q}$, so $z\in B_{r+1}^{p,q}$.
  3. It's clear from definitions that $Z_1^{p,q}=\ker\parens{G^pA^{p+q}\to G^pA^{p+q+1}}$ and that $B_1^{p,q}=\im\parens{G^pA^{p+q-1}\to G^pA^{p,q}}$. Part 3 follows.
  4. Suppose now that there exists $n,m\in\Z$ such that $F^nA^\bullet=A^\bullet$ and $F^mA^\bullet=0$ (so $m>n$). Fix any $p,q\in\Z$, and choose any $r>\max\{m-p,p-n+1,0\}$. Then, $$F^{p+r}A^{p+q+1}\subseteq F^mA^{p+q+1}=0\text{ and }F^{p-r+1}A^{p+q-1}\supseteq F^nA^{p+q-1}=A^{p+q-1},$$ so $Z_r^{p,q}=\parens{F^pA^{p+q}\cap\ker d+F^{p+1}A^{p+q}}/F^{p+1}A^{p+q}$, and $B_r^{p,q}=\parens{F^pA^{p+q}\cap\im d+F^{p+1}A^{p+q}}/F^{p+1}A^{p+q}$. With these descriptions stated, we obviously have a surjective map $F^p\hom^{p+q}(A^\bullet)\onto E_r^{p,q}$. The kernel of this map will be the cohomology classes $\alpha\in F^p\hom^{p+q}(A^\bullet)$ represented by a cycle $x\in F^{p+1}A^{p+q}$; that is, the kernel is exacly $F^{p+1}A^{p+q}$, so we get our desired isomorphism $G^p\hom^{p+q}\iso E_r^{p,q}$.

Before ending this section, I should maybe mention some standard terminology. The data summarized in the above theorem (i.e. objects $E_r^{p,q}$ with differentials of bidgree $(r,1-r)$ such that $E_{r+1}$ is the cohomology of $E_r$) is collectively known as a (cohomological) spectral sequence. For fixed $r$, the objects $E_r^{p,q}$ form the $r$th page (or $E_r$-page) of the sequence. In general, if $E_r^{p,q}$ only depends on $p,q$ for $r$ sufficiently large, then we denote this object by $E_\infty^{p,q}$. Hence, for the spectral sequence of a bounded filtered complex $A^\bullet$, we have $E_\infty^{p,q}=G^p\hom^{p+q}(A^\bullet)$. Spectral sequences are usually drawn as a 2d grid with $p$ increasing to the right, and $q$ increasing as you move vertically upwards.

Show that this spectral sequence is compatible with cup products in the sense that, on each page, we get an induced map $$\mapdesc{\smile}{E_r^{p,q}\by E_r^{s,t}}{E_r^{p+s,q+t}}{([x],[y])}{[x\smile y]}$$ such that $d_r(\alpha\smile\beta)=d_r(\alpha)\smile\beta+(-1)^{p+q}\alpha\smile d_r(\beta)$.
Actually, hold off on this exercise for now, and then do it specifically for the Serre spectral sequence construction later.

A Neat Application

Now that we’ve seen a way of constructing spectral sequences, let’s spend some time looking at their applications on topology. In this section, we’ll (re)prove one result one usually gets without spectral sequences, and then in the next section we’ll look into something more substantive. Namely, we’ll first show that singular and cellular cohomology agree.

Fix a CW-complex $X$, and let $X^k$ denote its $k$-skeleton. Let $C^\bullet(X)$ denote its singular cochain complex, so $C^n(X)=\Hom_{\Z}(C_n(X),\Z)$ where $C_n(X)$ is the free abelian group generated by maps $\Delta^n\to X$. We filter this by setting 12

\[F^pC^n(X)=\bracks{\phi\in C^n(X):\phi\vert_{C_n(X^p)}=0}=\ker\parens{C^n(X)\to C^n(X^p)},\]

where the map $C^n(X)\to C^n(X^p)$ is the natural restriction map. This is indeed a decreasing filtration, so we get a spectral sequence $E_{p,q}^0=G^pC^{p+q}(X)\implies\hom^{p+q}(X)$. We claim that $E_{p,q}^0\simeq C^{p+q}(X^{p+1},X^p)$, the group of relative cochains. Note that we have a homomorphism of short exact sequences

\[\begin{CD} 0 @>>> F^{p+1}C^{p+q}(X) @>>> C^{p+q}(X) @>>> C^{p+q}(X^{p+1}) @>>> 0\\ &@VVV @VVV @VVV\\ 0 @>>> F^pC^{p+q}(X) @>>> C^{p+q}(X) @>>> C^{p+q}(X^p) @>>> 0 \end{CD}\]

where the middle map is the identity, the right map is the natural restriction map, and left map is the unique one making the diagram commute. Now, since the middle map is an isomorphism, the snake lemma tells us that the left map is injective, and that its cokernel is isomorphic to $\ker(C^p(X^{p+1})\to C^p(X^p))$, so

\[E_0^{p,q}=G^pC^{p+q}(X)=F^pC^{p+q}(X)/F^{p+1}C^{p+q}(X)\simeq\ker\parens{C^{p+q}(X^{p+1})\to C^{p+q}(X^p)}=C^{p+q}(X^{p+1},X^p)\]

as claimed. Now, by definition, cohomology of this page gives relative cohomology, so $E_1^{p,q}=\hom^{p+q}(X^{p+1},X^p)$ 13. Recall that $\hom^{p+q}(X^{p+1},X^p)=0$ if $q\neq1$, so the only nontrivial differentials on the $E_1$ page are $d_1^{p,1}:\hom^{p+1}(X^{p+1},X^p)\to\hom^{p+2}(X^{p+2},X^{p+1})$. One easily checks that these agree with the differentials defining cellular cohomology, so the $E_2$ is given by

\[E^2_{p,q}=\twocases{\hom_{\text{cell}}^{p+1}(X)}{q=1}0.\]

There are no more nontrivial differentials past this point, so $E_2^{p,q}=E_\infty^{p,q}$. Finally, since each diagonal 14 only contains one nonzero object, we conclude that $\hom^p(X)\simeq E_\infty^{p-1,1}\simeq\hom^p_{\mrm{cell}}(X)$ 15, so singular and cellular cohomology agree.

Serre Spectral Sequence

In this section, I’ll need to assume more topology background that in the previous sections; in particular, you should know about fibrations and their long exact sequences in homotopy. Here, we’ll construct the Serre spectral sequence which is used to relate the (co)homologies of the base and fiber spaces of a fibration, to that of its total space. With that said, let’s just do it 16 17.

Let $$F\too E\xtoo\pi B$$ be a (weak/Serre) fibration with $B$ simply-connected. Then, there exists a spectral sequence $E_r^{p,q}$ with $E_2$-page $$E_2^{p,q}=\hom^p(B;\hom^q(F))\implies\hom^{p+q}(E).$$
For simplicities sake, assume that $B$ is a finite-dimensional CW-complex. To get the theorem for all CW-complexes, you can make a limit argument at the end. To then get the full theorem, you can use CW approximation. We won't bother writing either of those arguments out in detail.
Let $B^p$ denote $B$'s $p$-skeleton, and let $X^p=\inv\pi(B^p)$, so $X=\dirlim X^p$. Then, like before, we can filter $C^\bullet(X)$ by setting $F^pC^\bullet(X)=C^\bullet(X,X^{p-1})$ and so obtain a spectral sequence $E_0^{p,q}\implies\hom^{p+q}(X)$ with $E_1$-page $E_1^{p,q}=\hom^{p+q}(X^p,X^{p-1})$. Our goal is to calculate the $E_2$-page of this sequence. Namely, we will show that the differential $E_1^{p,q}\xto{d_1}E_1^{p+1,q}$ is "the same as" $$\Hom(\hom_p(B^p,B^{p-1}),\hom^q(F))\to\Hom(\hom_{p+1}(B^{p+1},B^p),\hom^q(F)).$$ Note that cohomology of the above is just $\hom^p(B;\hom^q(F))$, (cellular) cohomology with coefficients in $\hom^q(F)$. We will first show that the groups match up, i.e. that $\hom^{p+q}(X^p,X^{p-1})\simeq\Hom(\hom_p(B^p,B^{p-1}),\hom^q(F))$. Let $\bracks{D_\alpha^p}_{\alpha\in A}$ be the collection of $p$-cells of $B$, let $S_\alpha^{p-1}=\del D_\alpha^p$, and let $\phi_\alpha:D_\alpha^p\to B^p$ be the characteristic map of the $p$-cell $D_\alpha^p$ for each $\alpha\in A$. Then, $\hom_p(B^p,B^{p-1})$ is free abelian with basis $\{D_\alpha^p\}$, so $$\Hom(\hom_p(B^p,B^{p-1}),\hom^q(F))\simeq\Hom(\Z^{\oplus A},\hom^q(F))\simeq\prod_{\alpha\in A}\hom^q(F).$$ Now, define the spaces $(\wt D_\alpha^p,\wt S_\alpha^p)$ via the pullback squares $$\begin{CD} (\wt D_\alpha^p,\wt S_\alpha^{p-1}) @>\wt\phi_\alpha>> (X^p, X^{p-1})\\ @VVV @VVV\\ (D_\alpha^p, S_\alpha^{p-1}) @>\phi_\alpha>> (B^p, B^{p-1}) \end{CD}$$ Note that $\wt D_\alpha^p$ and $\wt S_\alpha^{p-1}$ are not literal disks/spheres, but instead look for like "disk x fiber" or "sphere x fiber." We claim that $$\prod_{\alpha\in A}\hom^{p+q}(\wt D_\alpha^p,\wt S_\alpha^{p-1})\simeq\hom^{p+q}(X^p,X^{p-1}).$$ Since $B$ is a CW-complex, there exists some open neighborhood $N\subset B^p$ containing $B^{p-1}$ that deformation retracts onto $B^{p-1}$. That is, there exists some homotopy $h_t:N\to N$ with $h_0$ the identity and $h_1$ a retraction onto $B^{p-1}$. Since $\pi$ is a fibration, letting $\wt N=\inv\pi(N)$, we can lift $h_t$ to a homotopy $\wt h_t:\wt N\to\wt N$ wtih $\st h_0$ the identity and $\st h_1$ a map whose image lies in $X^{p-1}$. From this, we conclude that the inclusion $X^{p-1}\into\wt N$ is a homotopy equivalence. This means that $\pull\hom(X^p,X^{p-1})\iso\pull\hom(X^p,\wt N)$. At the same time, excision shows us that $\pull\hom(X^p,\wt N)\simeq\pull\hom(X^p\sm X^{p-1},\wt N\sm X^{p-1})$, but the RHS is now $$\pull\hom\parens{\bigsqcup_{\alpha\in A}(\wt D_\alpha^p,\wt S_\alpha^{p-1})}\simeq\prod_{\alpha\in A}\pull\hom(\wt D_\alpha^p,\wt S_\alpha^{p-q}),$$ so we're happy. The next step is to now construct isomorphisms $$\eps_\alpha:\hom^{p+q}(\wt D_\alpha^p,\wt S_\alpha^{p-1})\iso\hom^q(F).$$ Let $\wt D^p\onto D^p$ be any fibration over a $p$-dimensional disk. Write $\wt S^{p-1}:=\partial D^p=D^{p-1}_-\cup_{S^{p-2}}D^{p-1}_+$ as a union of a northern and southern hemisphere. Then, cohomology of the triple $(\wt D^p,\wt S^{p-1},\wt D^{p-1}_+)$ gives an isomorphism $\hom^{p+q-1}(\wt S^{p-1},\wt D^{p-1}_+)\iso\hom^{p+q}(\wt D^p,\wt S^{p-1})$, and excision (remove the complement of $\wt D_-^{p-1}$) gives an isomorphism $\hom^{p+q-1}(\wt S^{p-1},\wt D_+^{p-1})\iso\hom^{p+q-1}(\wt D_-^{p-1},\wt S^{p-2})$. Combining these two gives, $$\hom^{p+q}(\wt D^p,\wt S^{p-1})\simeq\hom^{p+q-1}(\wt D_-^{p-1},\wt S^{p-2}).$$ Applying this to $\wt D_\alpha^p$ + a little bit of induction gives a map $$\eps_\alpha:\hom^{p+q}(\wt D_\alpha^p,\wt S_\alpha^{p-1})\iso\hom^q(\wt D_\alpha^0).$$ Now, $\wt D_\alpha^0$ is the fiber over some $0$-cell $D_\alpha$, which is not necessarily $F$ (the fiber over our chosen basepoint $*$). However, lifting a (contractible) path from $D_\alpha^0$ to $F$ gives a (canonical) isomorphism $\hom^q(\wt D_\alpha^0)\simeq\hom^q(F)$, so we're done comparing groups. It's now left to show that the below square (whose vertical maps are isomorphisms) commutes $$\begin{CD} \hom^{p+q}(X^p,X^{p-1}) @>d_1>> \hom^{p+q+1}(X^{p+1},X^p)\\ @VVV @VVV\\ \Hom(\hom_p(B^p,B^{p-1}),\hom^q(F)) @>>> \Hom(\hom_{p-1}(B^p,B^{p-1}),\hom^q(F)) \end{CD}$$ We won't bother doing this here because I'm lazy, so just trust me when I say this is the case. QED.
The assumption that the base is simply connected is sufficient for our purposes in this post, but not strictly necessary. More generally, whenever $F\to E\xto\pi B$ is a fiber sequence with $\pi_1(B)$ acting on $\ast\hom(F)$ trivially, we get the same spectral sequence. Even more generally, when $\pi_1(B)$ acts on $\ast\hom(F)$ nontrivially, one can still get a spectral sequence abutting to the cohomology of the base space, but the $\hom^p(B;\hom^q(F))$ in the $E_2$ page can no longer be interpreted as singular cohomology; one now has to consider "cohomology with local coefficients" or "cohomology of a local system (locally constant sheaf)".
You do note need to use integral cohomology. The same argument(s) give a spectral sequence with $E_2^{p,q}=\hom^p(B;\hom^q(F;A))implies\hom^{p+q}(E;A)$ for any abelian group $A$.

This is our first serious, readily applicable spectral sequence. Perhaps unsurprisingly, it turns out to be really useful, so let’s see it in action.

Hurewicz isomorphism

We’ll first use Serre’s spectral sequence to prove Hurewicz’s theorem that a spaces first nontrivial homotopy group and first nontrivial homology group coincide 18. Before proving this, we’ll first need to prove a lemma (also named Hurewicz) elucidating the connection between $\pi_1$ and $H_1$ 19.

$\hom_1(X)\simeq\ab{\pi_1(X)}$.
For any $x\in X$, fix some path $\lambda_x:I\to X$ from our basepoint $*$ to $x$. Let $\Delta^n$ denote the standard $n$-simplex, and note that $\Delta^1\simeq I=[0,1]$, so paths and singular 1-simplices are the same thing. Hence, it seems fruitful to consider the map $$\mapdesc \phi{\pi_1(X)}{\hom_1(X)}{[f]}{[f]}$$ send the homotopy class of a loop $f:I\to X$ (based at $*$) to its homology class as a singular 1-simplex $f:\Delta\to X$. We should probably start by showing that this map is well-defined. First note that if $f,g$ are loops in $X$ with concatenation $fg$, then, as singular 1-chains, $fg$ is homologous to $f+g$. This is because $fg-f-g$ is the boundary of the 2-simplex $\Delta^2\to\Delta^1\xto{fg}X$ given by first squashing two faces of the triangle onto the third and then applying the loop $fg$. Hence, to show that $h$ is well-defined, it suffices to show that nullhomotopic loops have trivial homology classes. Let $h_t:I\to X$ be a homotopy from the constant loop $h_0=*$ to $h_1$. View this as a map $h:I\by I\to X,(t,s)\mapsto h_t(s)$. Note that $I\by I$ is a square, and so cutting diagonally, we can view it as the union of two simplices $\sigma_1,\sigma_2$. When taking the boundary of $(\sigma_1-\sigma_2)$, the diagonal of the square will cancel out, and we'll be left with $h_1$ plus a bunch of constant simplices. Each constant 1-simplex is the boundary of the constant 2-simplex with the same image, so those are all homologically trivial. Hence, $h_1$ is homologically trivial as well, so $\phi$ is well-defined. $\phi$ is also clearly surjective since a 1-simplex is a cycle iff it's a loop. Since $\hom_1(X)$ is abelian, $\phi$ factors through a map $\ab\phi:\ab{\pi_1(X)}\to\hom_1(X)$, which we claim is an isomorphism (i.e. injective). Note that we have a map $\psi:C_1(X)\to\ab\pi_1(X)$ given on a simplex $\sigma:I\to X$ by $\psi(\sigma)=[\lambda_{\sigma(1)}\sigma\overline{\lambda_{\sigma(0)}}]$. This map vanishes on the boundary of 2-simplices, and so induces a homomorphism $\push\psi:\hom_1(X)\to\ab\pi_1(X)$. Finally, if $f:I\to X$ is a loop, then $\psi(h(f))=[\lambda_*f\overline{\lambda_*}]=[f]\in\ab\pi_1(X)$, so $h$ is injective and we win.

Alright, got that out of the way. Before proving Hurewicz, I should note that while I’ve only talked about spectral sequences in cohomology, spectral sequences in homology exist as well. In particular, there’s one associated to an increasing filtration of a chain complex, and this gives rise to a Serre spectral sequence in homology which, for a fibration $F\to E\to B$, looks like $\hom_p(B;\hom_q(F))\implies\hom_{p+q}(E)$ 20. This is what we’ll use in the below proof.

Let $X$ be a simply connected space. Then the first nontrivial homology and homotopy groups agree, i.e. given any $n\ge1$, if $\pi_k(X)=0$ for all $1\le k< n$, then $\hom_k(X)=0$ for all $1\le k< n$ and $\hom_n(X)\simeq\pi_n(X)$.
We induct on $n$. The base case $n=1$ holds since $X$ is assumed simply connected and $\hom_1(X)=\ab{\pi_1(X)}$. Now, suppose $n>1$. Note that $\pi_k(\Omega X)\simeq\pi_{k+1}(X)$ for all $k$, so $\pi_k(\Omega X)=0$ for $1\le k< n-1$. This means that $\hom_k(\Omega X)=0$ in the same range, and $\hom_{n-1}(\Omega X)=\pi_{n-1}(\Omega X)=\pi_n(X)$. With this information in mind, consider the Serre spectral sequence induced by the path fibration $\Omega X\into PX\to X$. Induction tells us that $\redhom_k(X)=0$ for all $k< n$, so the $E^n$-page of this spectral sequence looks like (all the relevant differentials before this page were trivial) $$\begin{array}{c | c c c c} \tbf q & \\ n-1 & \hom_{n-1}(\Omega X) & 0 & \dots & 0 & ? \\ n-2 & 0 & 0 & \dots & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & 0 & 0 & \dots & 0 & 0\\ 0 & \Z & 0 & \dots & 0 & \hom_n(X) \\\hline & 0 & 1 & \dots & n-1 & n & \tbf p \end{array}$$ and there's a differential $d^n_{n,0}:\hom_n(X)\to\hom_{n-1}(\Omega X)\simeq\pi_n(X)$. Since this sequence is concentrated in the first quadrant, this is the last nontrivial differential that the $(n,0)$ and $(0,n-1)$ spots participate in, so $E_{n,0}^\infty=E_{n,0}^{n+1}$ and $E_{0,n-1}^\infty=E_{0,n-1}^{n+1}$. At the same time, $PX$ is contractible, so $E^\infty_{p,q}=0$ for all $p,q$. Thus, $d^n_{n,0}$ must be an isomorphism in order to kill both the $(0,n-1)$ and $(n,0)$ slots. Hence, $\hom_n(X)\simeq\pi_n(X)$ as claimed.
Fix any $n>1$. We have $\pi_k(S^n)=0$ if $k< n$, and $\pi_n(S^n)=\Z$.

$\pi_4(S^3)=\zmod2$

For our final application of spectral sequences this post, we’ll compute a nontrivial homotopy group of a sphere. First note that the Hopf fibration $S^1\to S^3\to S^2$ gives $\pi_k(S^3)\simeq\pi_k(S^2)$ for all $k>2$, so last corollary already showed that $\pi_3(S^2)\simeq\Z$. This section, we’ll see that $\pi_4(S^2)\simeq\pi_4(S^3)\simeq\zmod2$. 21

First let $S^3\to K(\Z,3)$ be a map inducing an isomorphism on $\pi_3$. Let $X$ be the homotopy fiber of this map, and let $Y$ be the homotopy fiber of the map $X\to S^3$. Then, $Y\simeq\Omega K(\Z,3)=K(\Z,2)\simeq\CP^\infty$. Furthermore, the long exact sequence of the original fibration $X\to S^3\to K(\Z,3)$ shows that $\pi_k(X)=0$ for $k\le3$ (use that $\pi_3(S^3)\to\pi_3(K(\Z,3))$ is an isomorphism) and that $\pi_4(X)\simeq\pi_4(S^3)$. By Hurewicz, this means that $\hom_4(X)\simeq\pi_4(S^3)$ and we’ll compute this by looking at the Serre spectral sequence (in cohomology, where we have cup products) of the left fibration $\CP^\infty\to X\to S^3$. The $E_3$-page of this sequence looks like

\[\begin{array}{c | c c c c} 6 & \Z a^3 & & & \Z a^3x\\ 4 & \Z a^2 & & & \Z a^2x\\ 2 & \Z a & & & \Z ax\\ 0 & \Z1 & & & \Z x \\\hline & 0 & 1 & 2 & 3 \end{array}\]

Above, $x\in\hom^3(S^3)$ is a generator as is $a\in\hom^2(\CP^\infty)$. The cup product in cohomology let’s us use these to write down generators for the cohomology groups $\hom^p(S^3;\hom^q(\CP^\infty))$. All the groups in odd numbered rows are 0 as are all groups in columns $p\not\in{0,3}$. The nontrivial differentials are $d_3^{0,2q}:\Z a^q\to\Z a^{q-1}x$ where $q\ge1$. Since $X$ is 3-connected, we have $\hom^k(X)=0$ for all $k\le3$, and so $d_3^{0,2}$ must be an isomorphism, i.e. (we can choose $x$ s.t.) $da=x$ where by $da$ we really mean $d_3^{0,2}(a)$, but don’t want to write that every time. Now, using the fact that $d$ is a derivation, we have 22

\[d(a^2)=(da)a+a(da)=2ada=2ax\text{ and in general }d(a^q)=na^{q-1}da=qa^{q-1}x.\]

Thus, the differential $d_3^{0,2q}$ is really just multiplication by $q$. Since this is the last page with nontrivial differentials, we get that, on the $E_\infty=E_4$-page, the only nonzero object on the $n=5$ diagonal is $E_\infty^{3,2}\simeq\zmod2$ and that the $n=4$ diagonal is 0 everywhere. Thus, $\hom^4(X)=0$ and $\hom^5(X)=\zmod2$. In general, we get $\hom^{2k}(X)=0$ and $\hom^{2k+1}(X)=\zmod k$. Because these groups all have rank $0$, universal coefficients tells us that

\[\hom^k(X)=\Ext^1(\hom_{k-1}(X),\Z),\]

and so 23 we get that

\[\hom_n(X)\simeq\twocases{\zmod k}{n=2k\text{ is even}}0.\]

In particular, $\pi_4(S^2)\simeq\pi_4(S^3)\simeq\hom_4(X)\simeq\zmod2$.

Exercises 24

Let $S^n\to E\to B$ be a fibration with $B$ simply connected. Construct a long exact sequence $$\cdots\too\hom^{p+n}(B;\Z)\too\hom^{p+n}(E;\Z)\too\hom^p(B;\Z)\too\hom^{p+n+1}(B;\Z)\too\hom^{p+n+1}(E;\Z)\too\cdots$$ Use this sequence to show that if $S^n\to S^{n+k}\to S^k$ is a sphere fibration, then $n=k-1$.
Let $F\to E\to S^n$ be a fibration with $n>1$. Construct a long exact sequence relating the cohomology of $F$ to that of $E$. Use this to determine the cohomology of the loop space $\Omega S^n$.

Sepctral Sequence of a Double Complex

At this point, things start to slow down. We move away from topology and back into pure homological algebra in order to construct another type of spectral sequence. We won’t see examples of this one in this post, but we might in future posts.

Fix once again some ambient abelian category $\msA$, and let $A^{\bullet,\bullet}\in\CoCh(\CoCh(A))$ be some double complex. That is to say, we have a collection $A^{p,q}\in\msA$ of objects of $\msA$ with commuting horizontal $d^{p,q}:A^{p,q}\to A^{p+1,q}$ and vertical $\del^{p,q}:A^{p,q}\to A^{p,q+1}$ differentials.

\[\begin{matrix} d^2=0 && \del^2=0 && d\circ\del=\del\circ d \end{matrix}\]

Complexes are good for defining (co)homology, and the usual way we get (co)homology from a double complex is by passing to its total complex 25.

The total complex $\Tot(A^{\bullet,\bullet})\in\CoCh(\msA)$ has objects $$\Tot(A^{\bullet,\bullet})^n=\bigoplus_{n=p+q}A^{p,q}$$ with differential $$d^n=\sum_{n=p+q}\parens{d^{p,q}+(-1)^p\del^{p,q}}.$$

Directly computing the cohomology of the total complex can be tricky, but luckily it comes with a natural filtration, and hence a natural spectral sequence 26. This filtration is

\[F^p\Tot(A^{\bullet,\bullet})^n=\bigoplus_{\substack{n=i+j\\i\ge p}}A^{i,j}.\]

From this, we get a spectral sequence $E_r^{p,q}$ which, under mild assumptions (e.g. for each $n\in\Z$ there are only finitely many nonzero $A^{p,q}$ with $p+q=n$), converges to $\hom^{p+q}(\Tot(A^{\bullet,\bullet}))$. We claim that the $E_2$-page of this sequence is given by the “naive double cohomology”

\[E_2^{p,q}\simeq\hom^p_d(\hom^q_\del(A^{\bullet,\bullet}))\]

given by taking vertical cohomology followed by horizontal cohomology. One we show this, we’ll call it a day. The $0$th page is given by

\[E_0^{p,q}=F^p\Tot(A^{\bullet,\bullet})^{p+q}/F^{p+1}\Tot(A^{\bullet,\bullet})^{p+q}=A^{p,q},\]

with differential $d_0:E_0^{p,q}\to E_0^{p,q+1}$ equal to the vertical differential $\del$. Hence,

\[E_1^{p,q}=\hom^q_\del(A^{p,\bullet}).\]

Any $[a]\in E_1^{p,q}$ is represented by some $a\in A^{p,q}$ with $\del a=0$, so the differential $d_1:E_1^{p,q}\to E_1^{p+1,q}$ on the $E_1$-page acts on these representatives just like $d$ does. Thus, the $E_2$-page is indeed

\[E_2^{p,q}=\hom^p_d\parens{\hom^q_\del\parens{A^{\bullet,\bullet}}}\]

as claimed.

  1. Replace “bird” with something less ill-defined if you want ↩

  2. While writing this, I repeatedly felt the need to add examples/exercises, so things quickly became more hands on than I first planned ↩

  3. And because singular (co)homology is one of the few things I know I never want to bother developing on this blog (along with the basics of linear algebra, most of point-set topology, and maybe some other stuff) ↩

  4. Secretly, you can skip the first part on abelian categories. Immediately after writing it, I forgot that I wanted to work with an abstract category instead of just $R$-modules, and so had $R$-modules in mind as I wrote everything else (e.g. I talk about elements of objects of the category which is kind of a no-no in general). So um, there are a few option. You can just pretend we’re working with $R$-modules throughout (and everything will be fine especially since all the example computations are done with abelian groups), or if you want things to still work in general, you can use the (non-trivial) fact that every abelian category embeds in a category of $R$-modules (or maybe using Yoneda/functor-of-points type reasoning? I haven’t thought about this approach) ↩

  5. Just apply the universal property to $\alpha:=\mu\circ a=\mu\circ b$. ↩

  6. For intuition, in $\mathrm{Ab}$, monomorphisms are injective maps, so this is saying every subgroup should be a kernel (i.e. all quotients exist). Similarly, epimorphisms are surjective maps, so the image of every map should be the domain modulo some subgroup (i.e. first isomorphism) ↩

  7. If you’re reading this post, you should already know what these are. I’m just defining them here because I want this first section to stand alone as an introduction to abelian categories regardless of the fact that it fits into the broader context of this whole post. ↩

  8. I’ll likely say chain when I mean to say cochain many times below ↩

  9. From now on, I’ll start being a little more sloppy with my $d$’s, not always explitily giving them their upper indexing. ↩

  10. There’s some dubious reasoning here, but I’m only trying to build intuition so that’s fine ↩

  11. Don’t read the proof of this; do it for yourself. The only reason I have it typed up here is that I’ve never worked through it on my own before this. ↩

  12. This filtration always works anytime you can write $X$ as a direct limit of spaces $X=\dirlim X^p$, and is the one I alluded to way back in the beginning of this post. ↩

  13. If I were smart, I wouldv’e subtracted 1 when defining the filtration, so that this would read $\hom^{p+q}(X^p,X^{p-1})$ instead. ↩

  14. i.e. $\bracks{E_2^{p,q}:p+q=n}$ for some fixed $n$. ↩

  15. Secretely, we need that $X$ is finite (i.e. $X=X^n$ for some $n$) so the filtration is bounded. However, we can always write $X\approx\dirlim X^p$ as a direct limit of finite CW-complexes, and cohomology commutes with direct limits (i.e. $\pull\hom(\dirlim X^p)=\invlim\pull\hom(X^p)$), so we win by taking limits. ↩

  16. I probably should have mentioned this earlier, but as far as I’m concerned, all topological spaces $X$ are path-connected and based with basepoint denoted by $* \in X$. ↩

  17. If any of you know a nice way to get footnotes working inside of html blocks, please tell me ↩

  18. Secretly, non-simply connected spaces don’t exist. ↩

  19. Probably you know this result already, but I’ve never bothered to pay attention to a proof of it before, so it feels worth writing up. ↩

  20. Also worth mentioning that the differential $d^r$ on the $r$th page of a homological spectral sequence has bidegree $(-r, r-1)$. ↩

  21. By Freudenthal suspension, we actually get the stronger result that $\pi_{n+1}(S^n)\cong\zmod2$ for all $n\ge3$. ↩

  22. $a$ and $da$ commute because $a$ lives in even degree. Remember that $ab=(-1)^{\deg(a)\deg(b)}ba$ in general when taking cup products ↩

  23. I think you may need to use that $\hom_{k-1}(X)$ is finitely generated and so looks like $\Z^r\oplus\zmod{p_1^{k_1}}\oplus\dots\oplus\zmod{p_g^{k_g}}$ and then use that Ext splits over direct sums in the first factor ↩

  24. It feels weird having an “exercises” (sub)section, but I didn’t want to give the impression that these were under the Hurewicz (sub)heading ↩

  25. Unimportant technical detail: in general, abelian categories are only required to have finite direct sums (“biproducts”). However, if you have a really big double complex (i.e. $A^{p,q}\neq0$ even when $p<0$ and/or $q<0$), then formation of the total complex can involve infinite direct sums, and so may not always be possible. ↩

  26. Actually, two natural filtrations/spectral sequences, but I’ll only mention one of them ↩

You may also like...
comments powered by Disqus