Let’s prove and discuss one of my favorite theorems from algebraic topology. It gives a characterization of when a contravariant “homotopy functor” from topological spaces ¹ to sets is representable, i.e. is (isomorphic to one) of the form $F(X)=[X,S]$ where $S$ is $F$’s representing object, and the notation $[X,S]$ denotes the set of homotopy classes of maps $X\to S$. The nice part about this is that many nice/important spaces one encounters when studying algebraic topology are secretly just representing objects for some functor that people care about. Instead of constructing these spaces directly, one can infer their existence from Brown Representability, and then use properties of the functor they represent to understand them as objects. Vice versa, knowing that a functor is representable gives you additional control over its behavior/properties. This will make more sense later when I discuss some example applications. $ \newcommand{\CW}{\mathrm{CW}} \newcommand{\Top}{\mathrm{Top}} \newcommand{\Set}{\mathrm{Set}} \DeclareMathOperator{\Ho}{Ho} $

Before starting, I should probably make clear in what category we’re actually working. Based on the fact that I used the phrase “homotopy functor” and that I’m called a functor representable when it spits out homotopy classes of maps, possibly the first category that comes to mind is something like: objects are topological spaces and morphisms are homotopy classes of maps. I’ll call this the naive homotopy category of Top because it is not quite what we want; in addition to considering maps only up to homotopy, you also want to artificially invert weak equivalences ² so that they become isomorphisms. In order to not have to worry about annoyances coming from artificially adding morphisms, we’ll just work with CW complexes instead of arbitrary spaces. The point is Whitehead’s theorem says that weak equivalences already are honest-to-God homotopy equivalences for CW complexes, and CW approximation tells us that every topological space is weakly equivalent to a CW complex, so these two together tells us that the (non-naive) homotopy category is equivalent to the naive homotopy category restricted to CW complexes ³. Lastly, because we’re doing algebraic topology and because we’re not savages, we want to work in a category of based spaces/maps so throughout we’ll assume that every space $X$ we encounter has some chosen basepoint, which we’ll denote by $x\in X$ or $*\in X$ depending on what’s convenient, and every map $f:X\to Y$ respects basepoints (i.e. $F(*)=*$). Finally, we need to assume all our spaces are connected. With all that said, let $\push\CW$ denote the category whose objects are based connected CW-complexes, and whose morphisms are (based) homotopy classes of continuous maps ⁴. Hence, unless stated otherwise, assume all spaces below are based, connected CW complexes. ⁵

A Warmup

Before tackling the main theorem, let’s work through a case that is easy enough to do “by hand.” Namely, we’ll prove that first singular cohomology is represented by the circle, i.e. $\hom^1(X;\Z)\simeq[X,S^1]$. We know that $\hom^1(S^1;\Z)\simeq\Z$, so let $\alpha\in\hom^1(S^1;\Z)$ be a generator, and consider the map

where $[f]$ denote the equivalence class of a map $f:X\to S^1$. We aim to show that $T$ is a bijection. In fact, in this case, $\hom^1(-;\Z)$ is not just a functor to Set, but actually a functor to $\Ab$, so one may wonder if $T$ could end up being a group isomorphism and not just a bijection. This is in fact the case. Give $[X,S^1]$ the group structure it gets from $S^1\subset\C$ being a (topological) group; I’ll leave it as an exercise to show that this map $T$ is a homomorphism (this should just be definition chasing). Because the proofs of injectivity/surjectivity of $T$ that we will see are of different flavors, we will give them separately.

We first show that $T$ is injective.

To show that $T$ is surjective, we’ll first need a simple lemma.

This argument will have quite a bit more setup than the last. We start with a few observations. Note that Hurewicz + Universal Coefficients shows that $$\hom^1(X;\Z)\simeq\Hom(\hom_1(X;\Z),\Z)\simeq\Hom(\pi_1(X),\Z)$$ since $\Z$ is abelian. Under these isomorphisms, one sees that for $f:X\to S^1$, we have $T(f)(g)=\alpha(f\circ g)$ where $\alpha\in\Hom(\pi_1(S^1),\Z)$ is still the generator, and $T(f)\in\Hom(\pi_1(X),\Z)$ and $g:S^1\to X$. This perspective let's us rephrase surjectivity of $T$ as the ability to extend certain maps. Specifically, let $A=\bigvee_{\gamma\in\pi_1(X)}S^1_\gamma$ where each $S^1_\gamma$ is a copy of the circle $S^1$, and let $h:A\to X$ be a map s.t. the restriction $h_\gamma:=h\vert_{S^1_\gamma}:S^1_\gamma\to X$ satisfies $[h_\gamma]=\gamma$ for all $\gamma\in\pi_1(X)$. Now, let $\beta\in\hom^1(X;\Z)$ be an arbitrary cohomology class, and let $g_\beta:A\to S^1$ be a map such that $g_\beta\vert_{S^1_\gamma}:S^1_\gamma\to S^1$ is a degree $\beta(\gamma)$ map for all $\gamma$. Then, $\beta$ is in the image of $T$ iff there exists some $f_\beta:X\to S^1$ such that the following diagram commutes i.e. if we can extend $g_\beta$ to a map on $X$. In order to make this language of extension more natural, we replace $X$ with the mapping cylinder $M_h$ (this is legal since the projection $M_h\to X$ is a homotopy equivalence), and so assume that $h:A\to X$ is inclusion of a subcomplex. Finally, observe that $S^1$ is a $K(\Z,1)$, and so $S^1\simeq\Omega K(\Z,2)$ is (homotopically equivalent to) a loop space. With all that said, we can now actually prove this thing. Thinking of $S^1$ as a loop space, the map $A\xto{g_\beta}S^1\simeq\Omega K$ (with $K=K(\Z,2)$) gives rise to a homotopy $H_t:A\to K$ given by $H_t(a)=g_\beta(a)(t)$ (recall, a loop is a map $I\to K$, equal on the endpoints). Note that $H_1(a)=g_\beta(a)(1)=*$ since all loops are based, so $H_t$ is a nullhomotopy. By the previous lemma, this means $H_t$ is equivalently a map $CA\to K$. Similarly, $H_0(a)=*$ so $H_0$ extends to a constant map $X\to K$. Combining this with previous map gives us a map $G_0:X\cup CA\to K$ (constant on $X$, and $H_t$ on $CA$). This map is nullhomotpic via $G_t(x)=*$ for $x\in X$ and $G_t(a,s)=H_{s+(1-s)t}(a)$ for $(a,s)\in A\by I$. Now, $X\cup CA$ is a subcomplex of $CX$, and so the inclusion $X\cup CA\into CX$ satisfies the homotopy extension property. The constant map $\overline G_1:CX\to K$ extends the starting endpoint of the homotopy $G_{1-t}:X\cup CA\to K$, and so we can continue $\overline G_1$ to an entire homotopy $\overline G_{1-t}:CX\to K$ which extends $G_{1-t}$. In particular, $\overline G_0$ is a map $CX\to K$ extending the map $G_0:X\cup CA\to K$ which was constant on $X$; i.e., $\overline G_0$ is a homotopy $X\by I\to K$ which is constant at both endpoints; i.e. $\overline G_0$ is a map $X\to\Omega K\simeq S^1$. This is our desired extension $f_\beta$.

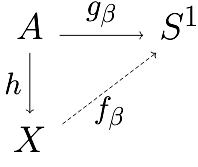
At last, we have shown that $[X,S^1]\simeq\hom^1(X;\Z)$ for connected $\CW$-complexes $X$. Now, in light of our discussion that the homotopy category of (based, connected) CW complexes is equivalent to that of (based, connected) topological spaces, it may be tempting to conclude from this that in fact $[X,S^1]\simeq\hom^1(X;\Z)$ for all based, connected topological spaces $X$. However, this is false. The point is that, in the homotopy category, weak equivalences are meant to be isomorphisms, but singular cohomology is not invariant under weak equivalences, so $\hom^1(-;\Z)$ isn’t a functor on $\Ho(\push\Top)$, the homotopy category on topological spaces. The correct functor on $\Ho(\push\Top)$ corresponding to singular cohomology on $\push\CW$ is $\hom^1(Z(-);\Z)$ where $Z(X)$ is a (functorial) $CW$ approximation of $X$.

Before moving onto Brown representability in full generality, it is worth mentioning an extension of the argument here. In this section, we showed that $[X,K(\Z,1)]\simeq\hom^1(X;\Z)$; later in this post, we’ll use Brown representability to say furthermore that, for any abelian group $G$ and $n\ge1$, we have $[X,K(G,n)]\simeq\hom^n(X;G)$. The isomorphism here is again given by pulling back a “universal cohomology class on $K(G,n)$” which is defined as the image of the identity map under the isomorphism

coming from Hurewicz + Universal Coefficients. If you read over the proof of surjectivity given here, it converts essentially immediately into a proof of surjective for general $K(G,n)$. The injectivity, however, made more usage of specific features of $S^1$ (e.g. it has a contractible universal cover) so one needs a different strategy to prove injectivity for arbitrary Eilenberg-Maclane spaces (although not when $n=1$).

The Theorem

Now, that we’re all warmed up, let’s get into the meat of things. We seek a characterization for when a (contravariant) functor $F:\push\CW\to\Set$ is representable. Let’s start by finding some necessary conditions, so fix a space $X$ and consider the functor $h_X=[-,X]:\push\CW\to\Set$; what are some general properties of $h_X$?

Before answering this, let’s introduce a bit of notation. Given a contravariant function $F:\push\CW\to\Set$ and an open embedding $i:U\into V$, we get a map $F(i):F(V)\to F(U)$. Given any $x\in F(V)$, denote its image $F(i)(x)\in F(U)$ as $x\vert_U$, taking inspiration from the notation for restricting functions. Now, returning to our functor $h_X$, it satisfies…

1. (Wedge Axiom) First, $h_X$ turns wedges (i.e. coproducts in $\push\CW$) into products. Symbolically, $$h_X(\bigvee_\alpha A_\alpha)=\sqbracks{\bigvee_\alpha A_\alpha,X}\simeq\prod_\alpha[A_\alpha,X]=\prod_\alpha h_X(A_\alpha),$$ since a map out of a coproduct is the same thing as a map out of each factor.
2. (Mayer-Vietoris Axiom) Secondly, we can glue together maps agreeing on an overlap. In other words, if $A=U\cup V$ and $u\in h_X(U),v\in h_X(V)$ are maps agreeing on $U\cap V$ (i.e. they have the same image under the maps $h_X(U)\to h_X(U\cap V)\from h_X(V)$, i.e. $u\vert_{U\cap V}=v\vert_{U\cap V}$), then they glue to some map $a\in h_X(A)$ (i.e. $a\vert_U=u$ and $a\vert_V=v$).

That’s all.

Note that the $X$ guaranteed by this theorem is necessarily unique up to unique isomorphism (e.g. by Yoneda). Similarly, the natural isomorphism $F\simeq h_X$ (which really goes the other way) is necessarily given by pulling back the “universal structure” $x\in F(X)=h_X(X)=[X,X]$ which is the element corresponding to the identity map $X\to X$. That is, it must be of the form

Finally, note that $F(*)={*}$ is a one-element set. This is because the wedge axiom tells us that $F(X\vee*)=F(X)\by F(*)$ but $X\vee*\simeq X$, so $F(X\vee*)=F(X)$ and the bijection corresponds to the projection map $F(X)\by F(*)\to F(X)$. This is only possible if $F(*)$ is a singleton.

With that said, how do we prove this thing? Well, we’re working with CW complexes which are basically determined by their homotopy groups, so maybe we should find a space $X$ with the correct homotopy groups. Note that, if $F$ is representable with representing object $X$, we have $\pi_n(X)=[S^n,X]=F(S^n)$.

Fix a contravariant functor $F:\push\CW\to\Set$ satisfying the wedge and Mayer-Vietoris axioms.

This may seem like a strong condition, but we’ll see that universal pairs are relatively easy to come by.

We construct $X$ from $Z$ by inductively attaching cells. Specifically, we seek pairs $(X_n,u_n)$ such that $Z\subset X_n$, the map $T_n=T_{u_n}:\pi_k(X_n)\to F(S^k)$ is an isomorphism for $0 < k < n$, and $T_n$ is surjective for $k=n$. We start with $n=1$ (We can't start with $n=0$ since $S^0$ is disconnected). Let $X_1=Z\bigvee_\alpha S^1_\alpha$ where $\alpha$ ranges over the elements of $F(S^1)$. By the Wedge axiom, there exists some $u_1\in F(X_1)$ with $u_1\vert_Z=z$ and $u_1\vert_{S^1_\alpha}=\alpha$ for all $\alpha\in F(S^1)$, so this gives $(X_1,u_1)$.
Now, suppose we have $(X_n,u_n)$ constructed, and we seek to construct $(X_{n+1},u_{n+1})$. Let $X_n'=X_n\bigvee_\alpha S^{n+1}_\alpha$ where $\alpha$ ranges over all $F(S^{n+1})$. Use the Wedge axiom to find some $u_n'\in F(X_n')$ such that $u_n'\vert_{X_n}=u_n$ and $u_n'\vert_{S^{n+1}_\alpha}=\alpha$. Then, $\pi_{n+1}(X_n')$ surjects onto $F(S^{n+1})$, but we don't yet have that $\pi_n(X_n')$ maps isomorphically onto $F(S^n)$. For each $\beta\in\ker\parens{\pi_n(X_n')\to F(S^n)}$, consider an $(n+1)$-cell $e^{n+1}_\beta$ and glue it to $X$ via an attaching map $\phi_\beta:\del e^{n+1}_\beta=S^n\to X_n'$ representing $\beta$ (i.e. $[\phi_\beta]=\beta\in\pi_n(X_n')$). Call the result of gluing all these cells $X_{n+1}$, i.e. $X_{n+1}$ is the pushout $$\begin{CD} \bigvee_\beta S^n_\beta @>\bigvee\phi_\beta>> X_n'\\ @VVV @VVV\\ \bigvee_\beta e^{n+1}_\beta @>>> X_{n+1} \end{CD}$$ By construction, $u_n'\vert_{S_\beta^n}=\pull\beta(u_n')=0$ for all $\beta$. Similarly, $F(\bigvee_\beta e^{n+1}_\beta)=0$ since this wedge is contractible, so Mayer-Vietoris let's us extend $u_n'$ to some $u_{n+1}\in F(X_{n+1})$. Now, because $X_{n+1}$ is formed by attaching cells of dimension $n+1$ to $X_n'$, we have that $\pi_k(X_n')\to\pi_k(X_{n+1})$ is an isomorphism for $k\le n-1$ and a surjection for $k=n$, so the same is true of $T_{u_{n+1}}:\pi_k(X_{n+1})\to F(S^k)$ by staring at the below commutative diagram. It is also clear that $T_{u_{n+1}}$ is still surjective from $\pi_{n+1}(X_{n+1})\to F(S^{n+1})$ essentially since the $S^{n+1}_\alpha$ from before have been left unchanged (gluing cells commutes with forming wedge products). Thus, we only need to show that $\pi_n(X_{n+1})\to F(S^n)$ is injective in order to be finished with the induction. Pick some $\gamma\in\ker\parens{\pi_n(X_{n+1})\to F(S^n)}$. Since the top map in the above diagram is surjective, this $\gamma$ comes from some $\beta\in\ker(\pi_n(X_n')\to F(S^n))$. However, by construction, any such $\beta$'s image in $\pi_n(X_{n+1})$ is trivial (it's represented by a map factoring through the contractible $e_\beta^{n+1}$), so $\gamma=0$ and $T_{u_{n+1}}$ is indeed injective.
With the induction done, let $X=\bigcup_{n\ge1}X_n$. We first seek to find some $u\in F(X)$ such that $u\vert_{X_n}=u_n$ for all $n$. Consider the mapping telescope $T$ of the inclusions $X_1\into X_2\into X_3\into\dots$ which is just the subcomplex $T=\bigcup_iX_i\by[i,i+1]$ of $X\by[1,\infty)$. We have that $X\by[1,\infty)$ deformation retracts onto $T$ (essentially since $X_i\by[1,\infty)$ deformation retracts onto $X_i\by[i,i+1]$) and so the natural projection $T\to X$ is a homotopy equivalence. Now, let $A\subset T$ be the union of the subcomplexes $\parens{X_i\by[i,i+1]}$ with $i$ odd along with the line $\{*\}\by[1,\infty)$. Let $B\subset T$ be the same with $i$ even. Then, $$A\simeq\bigvee_{i\ge1}X_{2i-1},\, B\simeq\bigvee_{i\ge1}X_{2i},\, A\cap B\simeq\bigvee_{i\ge1}X_i,\,\text{ and }A\cup B=T.$$ The wedge axiom gives some $a\in F(A)$ and $b\in F(B)$ such that $a\vert_{X_{2i-1}}=u_{2i-1}$ and $b\vert_{X_{2i}}=u_{2i}$ for all $i$. Furthermore, the fact that $u_i\vert_{X_j}=u_j$ for all $1\le j\le i$ shows us that $a\vert_{A\cap B}=b\vert_{A\cap B}$, so the Mayer-Vietoris axiom gives some $u\in F(T)$ s.t. $u\vert_{X_i\by\{i+1\}}=u_i$ for all $i$. Since $T\simeq X$, we can view this $u$ as an element of $F(X)$ s.t. $u\vert_{X_i}=u_i$ for all $i$.
Finally, to see that $(X,u)$ is indeed universal, use that the isomorphism $T_{u_n}:\pi_k(X_n)\to F(S^n)$ (say, $k< n$) factors as $$\pi_k(X_n)\to\pi_k(X)\xto{T_u}F(S^k).$$ The map $\pi_k(X_n)\to\pi_k(X)$ is an isomorphism for all $k < n-1$ so we must also have that $T_u$ is an isomorphism for $k < n-1$. Since $n$ is arbitrary, we win.

Whew. That was the brunt of the argument. We now show that maps to universal pairs can always be extended.

Now, we prove Brown Representability.

A natural question at this point is, “What is this useful for?” and so we’ll spend the rest of this post giving a partial answer to that.

An Application: CW Approximation

We’ll start with something simple, but kinda cute. Let $X$ be an arbitrary based, connected topological space. Then, we evidently get a contravariant functor $F:\push\CW\to\Set$ given by $F(A)=[A,X]$. It is clear that this satisfies the Wedge and Mayer-Vietoris axioms, so we get from this a CW complex $Z$ such that $[-,Z]\simeq[-,X]$. This $Z$ is called a CW Approximation of $X$. There are a couple things worth noting.

First, we get a map $f:Z\to X$ which is a weak equivalence. This map is the universal structure alluded to before, the image of the identity map under the isomorphism $[Z,Z]\simeq[Z,X]$. This being a weak equivalence comes from the fact that

with middle isomorphism coming from compositing with $f$.

Second, the formation of CW approximations is functorial. Indeed, if we a map $g:X\to Y$ between arbitrary based, connected topological spaces, then $g$ induces a natural transformation $\push g:[-,X]\to[-,Y]$. Letting $Z(X),Z(Y)$ denote their CW approximations, we get another natural transformation

Hence, by Yoneda (or by looking at the image of the identity in $[Z(X),Z(X)]$), $g$ must correspond to some map $Z(g):Z(X)\to Z(Y)$.

At last, our earlier claim that the homotopy category of (based, connected) topological spaces was equivalent to that of CW complexes has some justification ⁶.

An Application: Singular Cohomology

Next, we deliver on an earlier promise to show that $\hom^n(X;G)\simeq[X,K(G,n)]$ when $X$ is a (based, connected) CW complex. For this, we need to show that Singular cohomology satisfies the wedge and Mayer-Vietoris axioms. Showing that is satisfies the wedge axiom is left as an exercise if you haven’t seen it before; for Mayer-Vietoris, we apply the Mayer-Vietoris sequence. In particular, if $X=U\cup V$, then we get an exact sequence

where the second map gives the difference of the pullbacks of cohomology classes along the inclusion maps $U\cap V\rightrightarrows U,V$. Exactness of this sequence says exactly that if we have $u\in\hom^n(U;G)$ and $v\in\hom^n(V;G)$ restricting to the same element of $\hom^n(U\cap V;G)$, then they come from some $x\in\hom^n(X;G)$. Thus, Brown representability applies and we know that $\hom^n(X;G)\simeq[X,K]$ for some space $K$.

To see that $K$ is an Eilenberg-Maclane space, we simply observe that

Furthermore, any reduced cohomology theory $h^n$ will satisfy these axioms and so be of the form $h^n(X)=[X,K_n]$ for some sequence $K_n$ of spaces. One can verify that we must have $K_n\simeq\Omega K_{n+1}$ coming from the fact that $h^n(X)\simeq h^{n+1}(\Sigma X)$. One can also show that, conversely, given a so-called $\Omega$-spectrum $K_n$ - a sequence of spaces with (weak) homotopy equivalences $K_n\to\Omega K_{n+1}$ - the functors $h^n=[-,K_n]$ form a reduced cohomology theory.

An Application: Classifying Spaces

This application will be a bit more involved than the last two. In it, we’ll use Brown representability to define spaces which classify certain types of fiber bundles (e.g. real or complex vector bundles). We’ll essentially partition the class of fiber bundles by their structure groups (e.g. a rank $n$ real vector bundle has structure group $\GL_n(\R)$ since this what controls how we glue trivial bundles to get non-trivial ones). To this end, we define

The point of this free, transitive right action is that it causes the fiber space of $P$ to be homeomorphic to $G$ except they have “forgotten which point was the identity.” I should also mention that for $\pi:P\to B$ to be a principal $G$-bundle, we require that any local trivialization $h:\inv\pi(U)\iso U\by G$ intertwines the right action with right translation, i.e.

The main motivation for studying these (at least, as far as I’m concerned) comes from the following theorem which I will not prove.

So, for example, every complex vector bundle comes from some principal $\GL_n(\C)$-bundle. This theorem turns the problem of understanding various kinds of bundles into one of just understanding these principal $G$-bundles. With that said, let $B:\push\CW\to\Set$ be the functor ⁷ which assigns to a space $X$, the set $B(X)$ of its principal $G$-bundles up to their natural notion of equivalence ⁸.

Now, we claim that $B$ satisfies the wedge and mayer-vietoris axioms which will give the existence of a space $BG$ such that the set of principal $G$-bundles on $X$ (up to isomorphism) is in canonical bijection with the set $[X,BG]$ of (homotopy classes of) maps from $X$ into $BG$. This is a big deal. It is very nonobvious that such a space should exist.

It is easy to see that $B$ satisfies the wedge axiom. If I have bundles $\pi_\alpha:P_\alpha\to B_\alpha$ over a collection of spaces, then I can glue them all to get a bundle over their wedge $\bigvee B_\alpha$ ⁹. Conversely, any bundle over a wedge can be restricted to one over each factor. The Mayer-Vietoris axiom takes a little more work out, but is still not hard. It basically says that defining a bundle over $U\cup V$ is the same as giving bundles over $U$ and $V$ that agree on $U\cap V$. This is true. The main point in this is that the conditions of being a bundle are all local and so bundles are amenable to gluing constructions/arguments.

As a consequence of the paragraph above the exercise, we now know that our classifying spaces $BG$ exist for all topological groups $G$. As usual, the set $B(BG)=[BG,BG]$ has a universal structure corresponding to the identity map, and we call this the universal bundle $\pi_G:EG\to BG$. What properties do these spaces have?

The exercise shows that $\pi_n(BG)\simeq\pi_{n-1}(G)$ (i.e. $\pi_n(\Omega BG)\simeq\pi_n(G)$). In light of this, we will first show that indeed $G\simeq\Omega BG$ (already, this computation of homotopy groups shows that $BG\simeq K(G,1)$ when $G$ is a discrete group). Because of this. $BG$ is sometimes called a delooping of $G$.

Actually, we’ll first show that $EG$ is contractible because this will suffice to show that $G\simeq\Omega BG$. We have a fiber sequence

which induces a long exact sequence in homotopy

One can trace identifications to see that the maps $\pi_n(BG)\to\pi_{n-1}(G)$ above are exactly the isomorphisms $B(S^n)\iso\pi_{n-1}(G)$ from the exercise, so $\pi_n(EG)=0$ for all $n$. Since $EG$ is a CW-complex, this shows that it is contractible. Thus, $G$ is homotopy equivalent to the homotopy fiber of the constant map $*\to BG$, but this is just $\Omega BG$.

We now show a converse to some of what we’ve seen.

This proposition gives us a way of actually constructing these spaces. To end this post, I’ll sketch the construction of a space classifying complex line bundles.

Given a complex rank $n$ vector bundle $E\to B$, one would initially expect its structure group to be $\GL_n(\C)$ ¹⁰, but we can take it to be something smaller. In particular, using Graham-Schmidt (or whatever it’s called), you can give all locally trivial pieces orthonormal bases, and then your transition function lands in $U(n)$, the group of $n\by n$ unitary matrices ¹¹. In particular, the structure group of a complex line bundle can be taken to be $U(1)=S^1$. Thus, we seek a bundle $S^1\to E\to B$ with $E$ contractible. Well, if we let $B=\CP^n$, then we can take $E=S^{2n+1}$ and the natural quotient map $E\to B$ makes $E$ an $S^1$-bundle over $B$. That is, we have a bundle

for all $n$. These sequences are compatible in the relevant sense, so we can take limit as $n\to\infty$ ¹² to get a bundle

Now, $S^\infty$ is contractible (essentially because $\pi_k(S^n)=0$ when $n$ big and $k$ fixed), so this shows that $\CP^\infty\simeq BS^1$. In light of the first theorem in this section, this means that any complex line bundle $\pi:E\to B$ ultimately arises from some map $f:B\to\CP^\infty$ ¹³. However, we can say even more. Not only is $\CP^\infty$ a $BS^1$, it is also $K(\Z,2)$ ¹⁴ so we have isomorphisms

That is, the set (really group because of tensor products of line bundles) of isomorphism classes of (topological) complex line bundles on a space $X$ is isomorphic to the second integral cohomology group $\hom^2(X;\Z)$. Given a line bundle $\pi:E\to X$, its corresponding cohomology class $c_1(E)\in\hom^2(X;\Z)$ is called its (first) Chern class.