I have a vague vision in my head of a series of posts designed to help me, and maybe also you, understand (parts of) the relationship between a few objects of interests in algebraic number theory: elliptic curves, selmer groups, binary quartic forms, and modular forms 1. I don’t know the whole story encompassing these objects, but allegedly, they are all linked in one way or another, and I have soft plans to understand these links over the next $n$ days. To aid in this, I hope to write (medium length to long 2) posts on each of these objects, drawing attention to their relationships to each other, and also including some facts/results I find interesting even if they don’t necessarily lie at the intersection of the study of e.g. elliptic curves and quartic forms. It seems most appropriate to begin this series with elliptic curves since they are the main reason I care about any of the other stuff.
While trying to come up with a rough idea for what I was going to say in this post, I ran into the issue of what my definition of an elliptic curve should be. On the one hand, I don’t think I will need anything too fancy for the main things I want to talk about in these posts, so I could probably get away with saying an elliptic curve $E$ is the zero set of a polynomial of the form $E:y^2+a_1xy+a_3y=x^3+a_2x^2+a_4x+a_6$ and not worry about having to prove anything annoying. On the other hand, having access to things like Riemann-Roch and the Picard group is really useful for understanding the group structure on elliptic curves, but being able to use these things requires much more setup. In the end, I decided that since I have already said words like \spec and sheaf on this blog before, the added work needed to be able to say Riemman-Roch is worth it, so I’ll start with a quick and probably mostly unhelpful introduction to schemes 3, and then focus on curves 4.
Finally, just to make things clear, for the main purpose of this post (setting the basics of elliptic curves, so we can later see how they connect to some other things), you can probably just skip to the section titled “Elliptic Curves,” read from there, and take some things for granted. The parts before that section are mostly here for technical completeness and for me to see if I actually know anything about geometry 5.
- A Quick(ish) Introduction to Schemes
- Generalities on Algebraic Curves
- Elliptic Curves
- $\l$-adic Representations
A Quick(ish) Introduction to Schemes
We will begin with some motivation for the eventual definition of a scheme. This will motivation will take the form of a definition of a $\smooth$ manifold. Usually, one thinks of a $\smooth$ manifold $X$ as a topological space satisfying some technical conditions (e.g. must be Hausdorff and paracompact) which moreover, and most essentially, “locally looks like $\R^n$”. The standard way to make sense of this last condition, is to say that $X$ is covered by opens (i.e. charts) $\bracks{U_\alpha}_ {\alpha\in A}$ each coming with a homeomorphism $\phi_\alpha:U_\alpha\to\R^n$. However, this is not enough, because we want $X$ to be $\smooth$, so we require furthermore that the “transition functions” $\phi_{\alpha\beta}:\phi_\alpha(U_{\alpha\beta})\to\phi_\beta(U_{\beta\alpha})$ (here, $U_{\alpha\beta}:=U_\alpha\cap U_\beta$) defined by $\phi_{\alpha\beta}=\phi_\beta\circ\inv\phi_\alpha$ are $\smooth$ in the normal calculus sense (since they are maps between open subsets of $\R^n$). The point of having all these charts and smooth overlap conditions, is that they allow you to make sense of the notion of a smooth function $X\to\R$ because smoothness is a local condition and we already know what it means for a function $\R^n\to\R$ to be smooth.
This might make you wonder, if we really care about smooth functions $X\to\R$, why not start with these instead of starting with charts? One can do this, and this is closer to what one does in the algebraic setting. Still on the topic of manifolds, note that the presheaf
\[\smooth_{\R^n}(U)=\bracks{\text{smooth functions }f:U\to\R}\]on $\R^n$ is indeed a sheaf, and hence the pair $(\R^n,\smooth_{\R^n})$ form a so-called
There are a few things I should clarify. First, I never said what a morphism of ringed spaces is, and so the requirement that $(U,\ints{U_\alpha})$ be isomorphic to $(\R^n,\smooth_{\R^n})$ is not yet well-defined. Intuitively, a morphism $f:(X,\ints X)\to(Y,\ints Y)$ between ringed spaces should be a continuous map $X\to Y$ and a map of sheaves $\ints X\to\ints Y$, but these sheaves live on different spaces, so we need a way to transfer sheaves from one space to another. There are two natural ways to do this.
Hence, we have a choice in our definition of a morphism $(X,\ints X)\to(Y,\ints Y)$ of ringed space. It could either 8 be a pair $(f’,\sharp f)$ of a continuous function $f’:X\to Y$ and a morphism $\sharp f:\ints Y\to\push f\ints X$ or a pair $(f’,f^\flat)$ of a continuous function $f’:X\to Y$ and a morphism $f^\flat:\inv f\ints Y\to\ints X$. Thankfully for us, these two definitions are equivalent because of the following.
Now that we have a notion of morphism of ringed spaces, our earlier definition of a smooth manifold as a ringed space that looks locally like $(\R^n,\smooth_{\R^n})$ makes sense.
Now that we know what ringed spaces are and have seen how we can use sheaves to nicely describe spaces formed by gluing together ones we care about, let’s define schemes.
Schemes
First, to get this out of the way, a
A morphism of locally ringed spaces is a morphism $f:(X,\ints X)\to(Y,\ints Y)$ of ringed spaces such that the induced maps $\ints{Y,f(x)}\to\ints{X,x}$ are local (i.e. $\inv f(\mfm_x)=\mfm_{f(x)}$ where $\mfm_x\subset\ints{X,x}$ is the maximal ideal and similarly for $\mfm_{f(x)}\subset\ints{Y,f(x)}$).
Now, schemes are basically algebraic manifolds, except the phrase “algebraic manifold” already refers to something else. Our model space/protypical example will be the affine schemes $\spec A$ where $A$ is any (commutative) ring (with unity). Recall that $\spec A=\bracks{\text{prime ideals }\mfp\subset A}$ and we topologize it by giving it the Zariski topology whose closed sets are the ones of the form $V(I)=\bracks{\mfp\supset I}$ for $I\subset A$ an ideal. We need to give this space a structure sheaf $\ints A=\ints{\spec A}$ which we want to think of as the “sheaf of (regular) functions”. It is clear that we should have $\ints A(\spec A)=A$ 9. Similarly, given $a\in A$, the basic open $D(a)=\bracks{\mfp\in\spec A:a\not\in\mfp}$ (“points where $a$ does not vanish”) satisfies $D(a)\simeq\spec A_a$ (at least topologically), so we should have $\ints A(D(a))=A_a$. Now, because sheaves are defined locally, because these $D(a)$ for a base for the topology on $\spec A$, and because $D(a)\cap D(b)=D(ab)$, this actually uniquely characterizes a sheaf on $\spec A$, which we unsurprisingly call $\ints A$. That is,
One can give other, possibly more concrete, constructions of $\ints A$.
Any locally ringed space isomorphic to the pair $(\spec A,\ints A)$ is called an affine scheme. In general, a scheme is a (locally) ringed space $(X,\ints X)$ which is locally isomorphic to affine schemes. A morphism of schemes is just a morphism of the underlying locally ringed spaces.
It is generally useful to know when a scheme $S$ is affine because affine schemes are the easiest to work with. We will not say much about figuring this out in general except to claim without proof that if $S\into\spec A$ is a closed immersion (to be defined below), then $S$ is affine, and furthermore, $S\simeq\spec A/I$ for some (not necessarily radical) ideal $I\subset A$.
I should also mention that if $X$ is a fixed scheme, and $S$ is another scheme, then we let $X(S)$ denote the set of morphisms $S\to X$. If $S=\spec A$ is affine, then we also write $X(A)=X(\spec A)$ for this set. We call the set $X(S)$ the set of $S$-points of $X$. For example, if $X=\spec\Z[x_1,\dots,x_n]/(f_1,\dots,f_m)$ and $S=\spec A$, then
\[X(A)=\bracks{\spec A\to\spec\Z[x_1,\dots,x_n]/(f_1,\dots,f_m)}=\bracks{\Z[x_1,\dots,x_n]/(f_1,\dots,f_m)\to A}=\bracks{a_1,\dots,a_n\in A:f_i(a_1,\dots,a_n)=0\,\forall i}\]really should be thought of as the set of points of the vanishing set $V(f_1,\dots,f_m)$ with coordinates in $A$. If we are working with $Y$-schemes $X\to Y$ and $S\to Y$, then $X(S)$ only consists of the maps $S\to X$ which respect the given maps $X\to Y$ and $S\to Y$ (In this case, we really should denote the set $X_Y(S)$, but it’s usually clear from context what we mean).
Now, schemes are too general to successfully study all at once, so there’s a whole host of adjectives one can put in front of a scheme or morphism of schemes in order to make things more tractable. Usually, one spends weeks getting a feel for all these various adjectives, but we don’t have time for that, so I’ll just go ahead a define a few with little motivation/intuition.
The definition of a closed immersion is different from what one might expect because there is not a unique scheme structure on a closed subset of a scheme. For example, the closed set ${(2)}\subset\spec\Z$ is the underlying topological space for the closed subschemes $\spec\F_2\into\spec\Z$ and $\spec\Z/(4)\into\spec\Z$, but $\spec\F_2\neq\spec\Z/(4)$. The requirement that $\ints Y\to\push f\ints X$ be surjective mirrors the fact that, in the affine case, closed subschemes correspond to quotients of the ring of global functions.
There are other adjectives, like separated and proper, that I may throw around every now and then. Don’t worry about them too much. Maybe if I end up putting (a version of) this post online, I’ll come back here later and actually define them. I don’t feel like doing it yet.
Maps to Affine Schemes
It will be useful to prove a universal property for maps to affine space, so let’s do that.
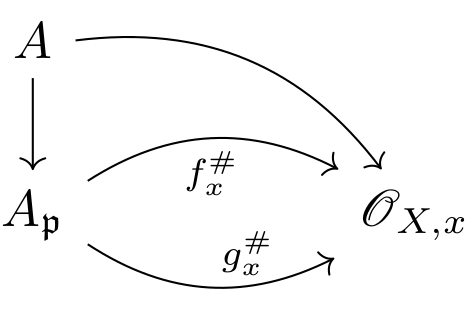
(Surjectivity) Pick some $\phi:A\to\ints X(X)$, and let $\{U_i\}_{i\in I}$ be an affine cover of $X$. Let $\phi_i:A\to\ints X(U_i)$ be the composition $A\xto\phi\ints X(X)\to\ints X(U_i)$, and let $f_i=\spec\phi_i:U_i=\spec\ints X(U_i)\to\spec A$, so, in particular, $\alpha(f_i)=\phi_i$. Note that $f_i\vert_{U_i\cap U_j}=f_j\vert_{U_i\cap U_j}$ for all $i,j\in I$ by injectivity of $\alpha$, so these $f_i$'s glue to give a global map $f:X\to\spec A$ and evidently, $\alpha(f)=\phi$.
Our main application of this will be in the case of the following space (possibly only when $n=1$).
Sheaf Cohomology
It is impossible to study geometry without making use of cohomology, so I guess I should take some time to define a cohomology theory on sheaves. Fix a topological space $X$. Then, the category $\Ab(X)$ of abelian sheaves is an abelian category (i.e. you can talk about kernels, cokernels, exactness, and all that good stuff). In particular, given a morphism $f:\msF\to\msG$ of sheaves on $X$, we define its kernel,cokernel,image to be the sheafifications of the following presheaves
\[(\pker f)(U)=\ker(\msF(U)\to\msG(U)).\] \[(\pim f)(U)=\im(\msF(U)\to\msG(U)).\] \[(\pcoker f)(U)=\coker(\msF(U)\to\msG(U)).\]As it turns out, one does not need to sheafify in the case of kernels, so $\ker f=\pker f,\pim f=(\pim f)^+,$ and $\pcoker f=(\pcoker f)^+$ where $^+$ is my notation for sheafification. With these defined, a sequence $\ms A\xto f\ms B\xto g\ms C$ of sheaves is called exact if $\ker g=\im f$. Note that this is weaker than requiring $\ker(\ms B(U)\to\ms C(U))=\im(\ms A(U)\to\ms B(U))$ for all open $U\subset X$.
Now that we have a notion of exactness, we can talk about a functor being left/right exact and then form derived functors. Of note, let $\Gamma:\Ab(X)\to X$ be the global sections functor $\Gamma(\msF)=\msF(X)$.
- You could show directly that given a short exact sequence $0\to\ms A\to\ms B\to\ms C\to0$ of sheaves, the sequence $0\to\ms A(X)\to\ms B(X)\to\ms C(X)$ remains exact. The main point here is that if you have a section $s\in\ker(\ms B(X)\to\ms C(X))$, then exactness at the sheaf level gives you local sections of $\ms A$ which map to (restrictions of) $s$ (i.e. by picking representatives of elements at the stalks), and these then glue by injectivity of $\ms A\to\ms B$.
- Alternatively, you could use the general fact that a functor is left exact iff it preserves kernels. Here, we clearly have that for $f:\ms A\to\ms B$ a morphism of sheaves, $\Gamma(\ker f)=\ker\parens{\Gamma(f):\ms A(X)\to\ms B(X)}$.
- A third possibility would be to show/observe that we have a natural isomorphism of functors $$\Gamma(\msF)=\Hom_{\Ab(X)}(\Z_X,\msF)$$ where $\Z_X$ is the constant sheaf on $X$ with stalks equal to $\Z$, and then use that $\Hom$-functors are usually left exact.
This is (almost) all we need to define the sheaf cohomology groups $\hom^i(X,\msF)$ as the right-derived functors of $\Gamma$. As a technical condition, in order for this construction to exist, we need to know that $\Ab(X)$ has enough injective, i.e. that every abelian sheaf on $X$ embeds in an injective sheaf. This is true and can be deduced from the fact that $\Ab$, the category of abelian groups, has enough injectives + a clever construction 10. We won’t do this in detail here partly because I’m lazy, and partly because we care mainly about curves, and so only care about cohomology in degrees 0,1 11. We will see later 12 that $\hom^1$ for the sheaves we care about (i.e. line bundles on curves) has a rather concrete description that will make it useful for computations. For now, the main things to know about cohomology are (1) that given a short exact sequence
\[0\too\ms A\too\ms B\too\ms C\too0\]of sheaves on $X$, we get a long exact sequence
\[0\too\hom^0(\ms A)\too\hom^0(\ms B)\too\hom^0(\ms C)\too\hom^1(\ms A)\too\hom^1(\ms B)\too\hom^1(\ms C)\too\dots\]in cohomology, and (2) cohomology for sheaves supported on a closed set $Z\subset X$ can be computed either on $Z$ or on $X$. Specifically,
The idea here is that there a special acyclic (i.e. higher cohomology vanishes) sheaves called “flasque sheaves,” and the pushforward of a flasque resolution of $\msF$ is a flasque resolution of $\push j\msF$ (with the same global sections), so their cohomologies are literally computed by the same complex. This is an example of the intuition/slogan that “sheaves on a closed subset $Z\subset X$ are the same thing as sheaves on $X$ which vanish outside of $Z$.” Because of this, we will often be lazy and omit the pushforward when considering sheaves on $X$ and sheaves on a closed subset in the same breath.
Before moving one, we’ll make one quick definition.
Line Bundles
Returning to our manifold motivation, (differential) geometers really seem to like vector bundles. If you’re studying a manifold, then its common to also try to understand its tangent bundle, cotangent bundle, exterior powers of these, etc. With this in mind, it might make sense to define algebraic vector bundles. To motivate the definition more, consider a topological vector bundle $p:E\to B$ of rank $n$. From $p$, one can construct the sheaf
\[\msE_p(U)=\bracks{s:U\to E:p\circ s=1_U}\]of local sections of $p$. Because $p$ is a vector bundle, it locally looks like $\R^n\by U\to U$, and so $\msE_p$ locally looks like $\ints U^{\oplus n}$ where $\ints U$ is the sheaf of (continuous or smooth or whatever) functions on $U$. In the algebraic context, we will take this sheaf $\msE_p$ as the definition of a vector bundle instead of the topological space $E$.
Let $(X,\ints X)$ be a ringed space. An $\ints X$-module $\msF$ is a sheaf on $X$ such that $\msF(U)$ is an $\ints X(U)$-module for all $U\subset X$, and such that the restriction maps $\msF(U)\to\msF(V)$ (when $V\subset U$) are compatible with restriction maps $\ints X(U)\to\ints X(V)$ in the evident sense. These form a category $\DeclareMathOperator{\Mod}{Mod}\Mod(X)=\Mod(X,\ints X)$ whose morphisms are exactly what you would expect.
Given a vector bundle $\ms E$ on $X$ and a point $x\in X$, the fiber of $\ms E$ above $x$ is the vector space
\[\ms E(x):=\ms E_x\otimes\kappa(x)=\ms E_x\otimes\ints{X,x}/\mfm_x=\ms E_x/\mfm_x\ms E_x\]whose dimension (over the residue field $\kappa(x)$) is equal to the rank of $E$ (since $\ms E_x\simeq\ints{X,x}^{\oplus\rank E}$). Given a section $s\in\msE(X)$ and a point $x\in X$, the value of this section at the point is the image $s(x)\in\ms E(x)$ of $s$ under the natural map
\[\ms E(X)\too\msE_x\too\ms E(x).\]I guess the main thing we need to know about line bundles is how they play with direct/inverse images and cohomology. I’ll just quote some results.
It is not the case that $\push f\msF$ is a line bundle when $\msF$ is. It is not even necessarily the case that $\push f\ints X$ is a line bundle (e.g. let $f$ be constant). Furthermore, the inverse image $\inv f\msG$ of an $\ints Y$-module does not even have to be an $\ints X$-module. To remedy this situation, we introduce
Projective Space
At this point, we know what schemes are, we know what cohomology is, and we even know what line bundles are. All we have left before moving on is to (sort of) see an example of a non-affine scheme. I won’t actually construct projective space where because that would be annoying, but I’ll at least tell you about it.
Fix a field $k$, and let $\DeclareMathOperator{\Sch}{Sch}\Sch_k$ denote the category of $k$-schemes, that is schemes $S$ equipped with a morphism $S\to\spec k$. It is clear that for any affine open $\spec A\subset S$ inside a $k$-scheme, $A$ is a $k$-algebra. Furthermore, given an $\ints S$-module $\msF$ on a $k$-scheme, its cohomology groups $\hom^i(\msF)$ are actually $k$-vector spaces. To study the geometry of curves, we want to understand their line bundles, so we introduce the following function $\DeclareMathOperator{\Set}{Set}P_n:\Sch_k\to\Set$
\[P_n(S)=\bracks{\parens{\msL,(s_0,\dots,s_n)}:s_0,\dots,s_n\in\Gamma(\msL)\text{ have no common zeros}}\]which spits out the collection of all sets of $n+1$ linearly independent sections of a line bundle on $P_n$. The main thing one needs to know about this functor is
One takeaway from the above theorem is that, whatever projective space is, we know that we can give a map into it by specifying a line bundle along with some linearly independent global sections of it. In particular, the identity morphism $\P^n\to\P^n$ corresponds to some line bundle $\ints{\P^n}(1)$ on $\P^n$ with $n+1$ linearly independent global sections (which we think of as “homogeneous coordinates” on $\P^n$). Via Yoneda-type reasoning, given any morphism $f:S\to\P^n$ of $k$-schemes, the data on $S$ determining this morphism is the line bundle $\msL:=\pull f\ints{\P^n}(1)$ with sections the pull-backs of the homogeneous coordinates of $\P^n$.
I do not think this is apparent from the above characterization, but it is a fact that $\P^n$ can be covered by $n+1$ affine opens, commonly denoted $D_+(x_i)$ for $i=0,\dots,n$. In fact, mirroring the classical construction of projective space,
\[D_+(x_i)\simeq\spec k\sqbracks{\frac{x_0}{x_i},\dots,\frac{x_{i-1}}{x_i},\frac{x_{i+1}}{x_i},\dots,\frac{x_n}{x_i}}\simeq\A^n_k\]for all $i$, and these affines are glued how you would expect. For example, to form $\P^1$, we glue $D_+(x_0)=\spec A\sqbracks{\frac{x_1}{x_0}}$ to $D_+(x_1)=\spec A\sqbracks{\frac{x_0}{x_1}}$ via the map $f:D_+(x_0)\to D_+(x_1)$ sending $x_0/x_1\mapsto x_1/x_0$. Put, perhaps more clearly, $\P^1$ is formed by gluing $\spec k[x]$ to $\spec k[y]$ (along the open subsets formed by removing the origin) via $x\leftrightarrow\inv y$.
Generalities on Algebraic Curves
We know can move away from the abstract generalities a bit and focus on something a little more down-to-earth.
One of the nice things about smooth curves is that their local rings are about as nice as you could ask for.
The above theorem tell us that the local rings $\ints{C,p}$ of a smooth curve are discrete valuation rings (when $p$ is a closed point), so for a closed point $p\in C$, we let $v_p:\units{k(C)}\to\Z$ denote the corresponding discrete valuation where $k(C)=\Frac\ints{C,q}$ (for any possibly non-closed $q\in C$) is the function field of $C$.
Divisors
Now, the main purpose of this section is to gain some understanding of the structure of line bundles on a smooth curve. To that end, we make the following definition.
Given two divisors $D,E\in\Div C$, we write $D\ge E$ if $v_p(D)\ge v_p(E)$ for all $p\in C$. We say a divisor $D$ is effective if $D\ge0$.
Fix a smooth curve $C$. Let $k(C)_ C$ denote the constant sheaf with stalks equal to $k(C)$. 13 Note that $k(C)_ C(U)=k(C)$ for all $U\subset C$ since $C$ is irreducible. Given a divisor $D\in\Div C$, let $\ints X(D)\subset k(C)_ C$ denote the subsheaf
\[\ints C(D)(U)=\bracks{f\in k(C):v_p(f)+v_p(D)\ge0\,\forall p\in U}.\]This is a line bundle (exercise 14) and the map $D\mapsto\ints C(D)$ gives a group homomorphism $\Div C\to\Pic C$, where $\Pic C$ is the group of line bundles (group operation given by tensoring). This map is surjective (we’ll see a dumb proof of this later) and its kernel is given exactly by the subgroup of principal divisors. To see this second part, note that if $f\in k(C)$, then multiplication by $f$ gives an isomorphism $\ints C(f)\iso\ints C$. Conversely, if $\ints C\iso\ints C(D)$, then $D=(1/f)$ where $f$ is the image of $1\in\Gamma(\ints C)$. With that said, let $\Cl C=\Div C/\units{k(C)}$ denote the Divisor class group of $C$. We’ve shown that $\Cl C\into\Pic C$, and we’ve claimed this is actually an isomorphism.
Hence, the study of line bundles on $C$ is tied up in the study of its divisors. We’re interested in understanding the sizes $h^0(D)=\dim_k\hom^0(\ints C(D)),h^1(D)=\dim_k\hom^1(\ints C(D))$ of the cohomology groups of $C$’s divisors. We’ll gain this understanding in the form of the Riemann-Roch formula which will appear in a few (sub)sections.
An important notion when studying divisors on curves, is the notion of a divisor’s degree. First, a bit of notation. Given a (possibly non-closed) point $x$ is a locally ringed space $(X,\ints X)$, the residue field at $x$ is the field
\[\kappa(x):=\ints{X,x}/\mfm_x\]where $\mfm_x\subset\ints{X,x}$ is the (unique) maximal ideal, i.e. $\kappa(x)$ is the residue field of the local ring at $x$. With that said
We wish to show that this descends to a map on class groups, i.e. that principal divisors have degree $0$. To do this, we will first show that nonzero elements of the function field $k(C)$ of $C$ are basically just morphisms $C\to\P^1$.
Let $f\in k(C)$ be nonzero. Let $Z,P\subset C$ be its set of zeros/poles, respectively. Then, $f\in\Gamma(C\sm P,\ints C$ and so determines a map $C\sm P\xto f\A^1_k$. Similarly, $1/f$ determines a map $C\sm Z\xto{1/f}\A^1_k$. We can glue these two maps together in other to form a map $C\xto f\P^1$. Using that $k(\P^1)=k(t)=\Frac k[t]$, we can recover $f\in k(C)$ from the morphism $C\to\P^1$ it defines as the image of $t$ under the map $k(\P^1)\to k(C)$ arising from this morphism (i.e. the induced map on stalks at the generic points).
Now, we’d like to be able to use morphisms between curves to relate divisors on them. To this end, let $f:X\to Y$ be a morphism (non constant) between smooth curves. We use $f$ to define two maps on divisors
\[\begin{matrix} \push f:& \Div X &\too& \Div Y && \pull f:&\Div Y &\too& \Div X\\ &[p] &\longmapsto& [\kappa(p):\kappa(f(p))]\cdot[f(p)] &&& [q] &\longmapsto& \sum_{p\to q}e(p/q)\cdot[p] \end{matrix}\]where $e(p/q)=v_p(t_q)$ where $t_q\in\ints{Y,q}$ is a uniformizer. Furthermore, since $f$ is non-constant (and all curves are assumed irreducible), it must be surjective (its image is an irreducible subset of a 1-dimensional space and bigger than 1 point). From this, we can conclude that $f$ maps $\eta_X$, the generic point of $X$, to $\eta_Y$, the generic point of $Y$. This is because the generic point of a space (which always exists for irreducible schemes) is the unique point contained in all of its open sets and so
\[\inv f(\eta_Y)=\inv f\parens{\bigcap_{W\ni\eta_Y}W}=\bigcap_{W\ni\eta_Y}\inv f(W)\ni\eta_X\]where we used surjectivity of $f$ to know that $\inv f(W)\neq\emptyset$ for every open set $W$ (containing $\eta_Y$). The upshot of this is that $f$ induces a map $k(Y)=\ints{Y,\eta_Y}\to\ints{X,\eta_X}=k(X)$ on function fields, and so we define $\deg f=[k(X):k(Y)]$. Now, we get the following theorem.
Differentials
Our next aim is to construct the so-called canonical bundle which will be a non-arbitrary line bundle we can write down for any smooth curve $C$. Fix a smooth curve $C$ over a field $k$.
For an affine open $\spec A\subset C$, let $\Omega_{A/k}$ denote the module of (Kahler) differentials which is the $A$-module generated by the symbols $\d a$ for all $a\in A$ subject to the relations
- $\d c=0$ if $c\in k$
- $\d(a+b)=\d a+\d b$
- $\d(ab)=a\d b+b\d a$
From a previous exercise, the $A$-module $\Omega_{A/k}$ gives rise to an $\ints A$-module $\wt{\Omega_{A/k}}$ on $\spec A$. Because formation of the module of differentials plays well with localizations 15, we can glue together the various sheaves $\wt{\Omega_{A/k}}$ to get a global sheaf $\omega_C=\Omega_{C/k}$ of differentials on $C$.
Differentials are useful in differential topology/geometry, so this sheaf is probably rather important. In case this quantity pops up again later, let’s go ahead and define the genus of $C$ to be $h^0(\omega_C):=\dim_k\hom^0(\omega_C)$ the dimension of global sections of $\omega_C$.
Now, one of the main utilities of differentials in algebraic geometry is their appearance in the following surprising and very useful theorem.
Originally, I planned on giving a proof of this theorem, but sadly, I think doing so would send us too far afield. Usually one proves a vast generalization of the above applying to higher dimensional schemes and far more sheaves than just bundles, but carrying this out would require more than a subsection of a blog post. There is a simpler proof just in the case of curves, but even it is too involved for me to justify reproducing here, so uh, just believe me on this one.
Riemann-Roch
Now, given Serre duality 16, proving Riemann-Roch will be child’s play. In general, “Riemann-Roch” type theorems consist of two parts. The first part is a formula, usually of the form $\chi(\msF)=f(\msF)+\chi(\ints X)$, for computing the Euler characteristic of a vector bundle in terms of that of the structure sheaf. In a sense that is hard to make precise, the function $f$ usually only depends coarsely on $\msF$ 17. The second part is a formula for $\chi(\ints X)$. We will begin, perhaps unsurprisingly, with the first part.
For the second part, we need to calculation $\chi(\ints C)=h^0(\ints C)-h^1(\ints C)$. We know from Serre duality that $h^1(\ints C)=h^0(\omega_C)=g$, so we really just need to calculate $h^0(\ints C)$. To do this, I’ll need to make explicit an assumption that I have been making in my head this whole time. The stated definition of curve allows for schemes like the affine line $\A^1_k$, but this is space, for example, is somehow incomplete (think “non-compact”). Now, topological compactness is not as useful a notion for schemes as it is for manifolds; for example, all affine schemes are compact 18, but $\A_k^n$ should not be considered complete since it is the analogue of $\R^n$. Hence, the right notion of algebraic compactness/completeness will be something else. For our purposes, it suffices to reason as follows: projective space $\P_k^n$ should be “algebraically compact” (& also “algebraically Hausdorff”), so if $C$ if complete, then the image of any map $C\to\P_k^n$ should be “algebraically compact” as well (since $C$ is), but this is just saying that the image should be closed (since $\P_k^n$ is “algebraically compact and Hausdorff”), so we say a curve $C$ is complete if the image of any morphism $C\to\P_k^n$ is closed.
The correct notions of “algebraically compact” and “algebraically Hausdorff” are being proper and separated, but for out purposes, completeness as just defined suffices 19. From now on 20, assume all curves are complete. With this assumption made
Thus, $\chi(\ints C)=1-g$. In summary, the takeaways are
\[\begin{align*} \chi(\ints C(D))=\deg D+1-g && h^1(\ints C(D))=h^0(\omega_C(-D)) \end{align*}\]where, given a line bundle $\msL$, $\msL(D)$ is shorthand for $\msL\otimes\ints C(D)$. Here are two consequences of the work that we have done.
Worth noting: contained in the above proof is an argument for the fact that divisors with negative degrees have no nonzero global sections (any global section gives an effective divisor and you can’t have an effective divisor of negative degree).
Elliptic Curves
That was quite a bit longer than I originally intended, but we made it. We can now turn our attention to the actual intended focus of this post: elliptic curves. Fix a field $k$.
This definition may be different from one you have seen before, so we will first show that it is actually the same as the classical one corresponding to the vanishing set of a cubic polynomial.
Fix an elliptic curve $E/k$. For any $n\in\Z$, let $D_n=n[\infty]\in\Div E$. Note that the canonical bundle $\omega_E$ is of degree $\deg\omega_E=2g(E)-2=0$ and has a nonzero global section $s\in\hom^0(\omega_E)$. Hence, $\omega_E=\ints E(s)$ where $(s)\in\Div E$ is an effective divisor of degree $0$, i.e. $\omega_E\simeq\ints E$ is trivial. Now, applying Riemann-Roch to the divisor $D_n$ defined before, we have
\[h^0(\ints E(D_n))=h^0(\ints E(-D_n))-h^0(\ints E(D_n))=\deg D_n+\chi(\ints E)=n\]for all $n\ge1$ (since divisors with negative degree have no global sections). The constant $1$ function lives in $\hom^0(\ints E(D_n))$ for all $n\ge0$ (and generates it when $n=0$), so we can complete it to basis $\bracks{1,X}$ of $\hom^0(\ints E(D_2))$ which we then in turn complete to a basis $\bracks{1,X,Y}$ of $\hom^0(\ints E(D_3))$. Necessarily, $X$ has a double pole at $\infty$ (since $h^0(\ints E(D_n))=1$ for $n\in\bits$) and similarly $Y$ has a triple pole at $\infty$. Now, note that $\bracks{1,X,Y,X^2,XY}\subset\hom^0(\ints E(D_5))$ and we claim that these form a basis. This is because they all have different orders of vanishing at $p$, so for any $c_0,c_2,\dots,c_5\in k$, not all zero, we have
\[v_p(c_0+c_2X+c_3Y+c_4X^2+c_5XY)=\min\bracks{i:c_i\neq0}\le5\implies c_0+c_2X+c_3Y+c_4X^2+c_5XY\neq0.\]Now, $\hom^0(\ints E(D_6))$ contains the 7 elements $1,X,Y,X^2,XY,Y^2,X^3$ which therefore must satisfy some nontrivial linear relation of the form 21
\[aY^2+a_1XY+a_3Y=bX^3+a_2X^2+a_4X+a_6.\]Necessarily, two of the involved functions (those with nonzero coefficient) must have the same valuation at $P$, so $a,b\neq0$. We can divide through by $b$ to assume that $b=1$, and then replace $X,Y$ with $aX,aY$ to obtain
\[a^3Y^2+a_1a^2XY+a_3aY=a^3X^3+a_2a^2X^2+a_4aX+a_6.\]Finally, dividing by $a^3$, we see that our elliptic curve $E$ satisfies a relation of the form
\[\label{wform}\begin{align}Y^2+a_1XY+a_3Y=X^3+a_2X^2+a_4X+a_6.\end{align}\]I just said finally, but you potentially expected a simpler looking end result. This is the best we can do over an arbitrary field $k$, but if we further suppose that $\Char k\neq2,3$ then we can (simultaneously) replace $X$ by $(X-3a_1^2-12a_2)/36$ and $Y$ by $(Y-(a_2X+a_3)/2)/216$ 22 to get a relation of the form $Y^2=X^3+aX+b$.
Before talking about the more arithmetic side of elliptic curves, I would like to explain to what extent these relations define the curve $E$, so fix $a_1,a_2,a_3,a_4,a_6\in k$ such that (\ref{wform}) holds. Then, we claim that $\parens{\ints E(D_3),(1,X,Y)}$ determines a morphism $f:E\to\P_k^2$. We need to check that $1,X,Y$ have no common zeros. Since these generate $\hom^0(\ints E(D_3))$, it suffices to check that there’s no (closed) $p\in E$ s.t. $s(p)=0\in\ints E(D_3)(p)\simeq\kappa(p)$ for all $s\in\hom^0(\ints E(D_3))$. To see this, consider the exact sequence
\[0\too\ints E(-p)\too\ints E\too\ints p\too0.\]Twist by $D_3$ (i.e. tensor with $\ints E(D_3)$) and look in cohomology to get
\[0\too\hom^0(\ints E(D_3-p))\too\hom^0(\ints E(D_3))\too\kappa(p)\too\hom^1(\ints E(D_3-p))=0,\]where the last equality comes from Serre duality. The map $\hom^0(\ints E(D_3))\too\kappa(p)$ above is the evaluation map, so we see that it is surjective, i.e. that some section has nonzero evaluation at $p$. Hence, we do get a morphism $f:E\too\P_k^2$, and further analysis can be used to show that it is a closed embedding. Once you know this, one can show that the section $X,Y$ of $\ints E(D_3)$ extend to global sections of the line bundle $\ints{\P_k^2}(1)$ on $\P^2$ (i.e. that $X,Y$ are really linear functions on $\P^2$). Hence, the relation (\ref{wform}) is really prescribing a way to write $E$ as a hypersurface in $\P^2$ (i.e. $E$ is the vanishing set of the homogenization of that polynomial)
Group Law
Now, the main source of interest in elliptic curves ultimately stems from the fact that their rational points form a group (actually, their $S$-points for any $k$-scheme $S$ do). We will describe how in this section.
Let $E/k$ be an elliptic curve with chosen basepoint $\infty\in E(k)$. Let $\Pic^0(E)\subset\Pic E=\ker\deg$ be the subgroup of (linear equivalence classes of) degree $0$ divisors. Consider the map
\[\mapdesc f{E(k)}{\Pic^0E}{p}{[p]-[\infty]}.\]Let $X,Y\in\hom^0(\ints E(3[\infty]))$ be as in the previous section. We aim to show that the above map is a bijection. This will allows us to pullback the group structure on $\Pic^0E$ to one on $E(k)$. We first show injectivity. Suppose that we have $p,q\in E(k)$ such that $[p]-[\infty]=[q]-[\infty]$ so $[p]=[q]$. Consider the exact sequence
\[0\too\ints E(p-q)\too\ints E(p)\too\ints q\too0\]This gives an injection $\hom^0(\ints E(p-q))\into\hom^0(\ints E(p))$. If $p\neq q$, then every section of $\ints E(p-q)$ must vanish at $q$, but $\hom^0(\ints E(p))$ is generated by the nowhere vanishing section $1$, so $\hom^0(\ints E(p-q))=0$ in this case which shows that $[p]\neq[q]\in\Cl E$ if $p\neq q\in E$.
Now, we show that $f$ is surjectivity. Let $D\in\Div E$ be a degree 0 divisor. Then, $D+[\infty]$ is degree 1, so there’s some nonzero global section $s\in\hom^0(\ints E(D+[\infty]))$. As usual, this means that $D+[\infty]$ is equivalent to some degree 1, effective divisor $E$ which must be of the form $E=[p]$ for some $p\in E(k)$. Thus, $D=[p]-[\infty]=f(p)$, so $f$ is bijective.
This allow us to define a group law on $E(k)$ via $p+q=\inv f(f(p)+f(q))$. As constructed, this group law is potentially arbitrary. However, one can show that it is actually induced from a morphism $m:E\by E\to E$ of $k$-schemes. In fancier words, this group law is a manifestation of the fact that $E$ is a $k$-group scheme 23. We will use without proof the existence of the morphism $m$.
- The basepoint $\infty\in E(k)$ is the identity element.
- For any 3 points $p,q,r\in E(k)$ "lying on a line" (i.e. $p+q+r=(s)$ for some $s\in\hom^0(\ints E(D_3))$), we have $$p+q+r=0.$$
Isogenies
Since $E,E’$ are 1-dimensional, irreducible, we either have $\phi(E)=\infty’$ or $\phi(E)=E’$ for any isogeny $\phi$. Like before, given a non-constant isogeny $\phi:E\to E’$, we let $\deg\phi$ denote the degree of the field extension $k(E)/\pull\phi k(E’)$.
Unless otherwise stated, assume that basically all isogenies below are nonzero.
One nice properties of isogenies is that they are automatically group homomorphisms.
The above shows that isogenies basically correspond to homomorphisms between Picard groups. Under this correspondence, an isogeny $\phi:E_1\to E_2$ is paired with the homomorphism $\push\phi:\Pic^0E_1\to\Pic^0E_2$. However, there is another homomorphism of Picard groups naturally associated to $\phi$: the pullback $\pull\phi:\Pic E_2\to\Pic E_1$, so this too should correspond to some isogeny.
Now, let $\phi:E_1\to E_2$ be an isogeny. The composition $\phi\circ\wh\phi:E_2\to E_2$ corresponds to the map $\push\phi\pull\phi:\Pic^0E_2\to\Pic^0E_2$ which is just multiplication by $(\deg\phi)$. Hence, $\phi\circ\wh\phi:E_2\to E_2$ is also multiplication by $\deg\phi$. We claim the same is true for the other composition $\wh\phi\circ\phi:E_1\to E_1$, i.e. that this is multiplication by $(\deg\phi)$. To see this, note that
\[(\wh\phi\circ\phi)\circ\wh\phi=\wh\phi\circ(\deg\phi)=(\deg\phi)\circ\wh\phi\]where the last equality comes from $\wh\phi$ being a homomorphism. Since $\wh\phi$ is surjective, we conclude that $\wh\phi\circ\phi=\deg\phi$ (as functions). As a consequence of the last exercise, we get
We can also show that $\deg\phi=\deg\wh{\phi}$ in general. From our above calculations on compositing an isogeny with its dual, this will follow from the following.
For the claim that $\wh{\wh\phi}=\phi$, this follows from the fact that $$\phi\circ\wh\phi=m=\wh m=\wh{\phi\circ\wh\phi}=\wh{\wh\phi}\circ\wh\phi=\deg\wh\phi.$$
Torsion Points
We now turn to understanding the structure of torsion points of an elliptic curve. In order to have a chance of getting nice results, fix an algebraically closed field $k$, and let $E/k$ be an elliptic curve. Let $E(k)[m]=\ker(m:E(k)\to E(k))$ denote the set of $m$-torsion points of $E(k)$ (note: since $k$ is algebraically closed, $E(k)$ is the set of all closed points) where $m\ge1$ is an integer. Our understanding of $E(k)[m]$ will rest on the following lemma relating the algebra of a morphism to its geometry.
Hence, given some $q\in V$ (corresponding to a prime $\mfp\in\spec A$), determining $\inv\phi(q)$ is the same as determining the primes $\mfP\in\spec B$ lying above the given $\mfp\in\spec A$. Since every prime in a purely inseparable extension of Dedekind domains completely ramifies, as far as determining the set $\inv\phi(q)$ is considered, we lose no information if we assume that $\Frac B=k(C_1)$ is separable over $\Frac A=k(C_2)$. It is now a standard result from the theory of Dedekind domains that in any such situation, a (nonzero) prime $\mfp\in\spec A$ factors in $B$ as a product $$\mfp B=\prod_{i=1}^g\mfP_i^{e_i}$$ of primes $\mfP_i\in\spec B$ with $n=[k(C_1):k(C_2)]=\sum_{i=1}^ge_if_i$ where $f_i=[B/\mfP_i/A/\mfp]$. Furthermore, the ramification indices $e_i$ are all equal to $1$ except for the (finite set of) primes dividing a certain "discriminant ideal" $\Delta_{B/A}\subset A$. Thus, we see that $\#\inv\phi(q)=\deg_s\phi$ for any (nonzero) $q$ in the open set $\spec A\sm V(\Delta_{B/A})$, and so we win.
In the previous section we calculated that $\deg m=m^2$ (where $m$ is denoting both an integer and the multiplication by that integer map). With this in mind, fix any nonzero $m\in\Z$ such that $p:=\Char k\nmid m$. In this case, multiplication by $m$ is separable, so we get that 24
\[\# E(k)[m]=\#\inv m(\infty)=m^2\]Let $G=E(k)[m]$. For any $d\mid m$, let $G[d]$ denote its $d$-torsion subgroup, so $G[d]=E(k)[d]$. Thus, $G$ is an abelian group of size $m^2$ whose $d$-torsion subgroup has size $d^2$ for all $d\mid m$. An argument inducting on the number of primes dividing $m$ then shows that this implies that $G\simeq\zmod m\oplus\zmod m$.
Now, what if $m=p^e$ for some $e\ge1$ (Here, we’re assuming $p=\Char k\neq0$)? In this case, consider the $p$th power Frobenius map $\phi:E\to E$ which is the morphism $E\to E$ corresponding to the $p$ power map $k(E)\to k(E)$ on $E$’s function field 25. This map visibly has degree $p$ and separable degree $1$, so we see that
\[\# E[p^e]=\deg_s[p^e]=\deg_s(\wh\phi\circ\phi)^e=(\deg_s\wh\phi)^e\in\bracks{1,p^e}\]where the ambiguity at the ends rests upon whether $\wh\phi$ is separable or inseparable. In the case that it is separable, $E[p^e]$ is a group of order $p^e$ whose $p^n$-torsion subgroup is of order $p^n$ for all $n\le e$. Another easy induction argument shows that this implies that $E[p^e]\simeq\zmod{p^e}$.
All in all, we have shown the following.
- If $m\neq0\in k$, i.e. if $p\nmid m$, we have $$E[m]=\Zmod m\oplus\Zmod m.$$
- If $\Char k=p>0$, then one of the following is true. Either $$E[p^e]=\{\infty\}$$ for all $e\ge1$, or $$E[p^e]=\Zmod{p^e}$$ for all $e\ge1$.
$\l$-adic Representations
To end this monster of a blog post, we will show how to use an Elliptic curve $E/\Q$ to construct an $\l$-adic representation of the absolute Galois group $G_\Q:=\Gal(\Qbar/\Q)$.
Fix an elliptic curve $E/\Q$. Note that the set (really, group) $E(\Qbar)$ (morphisms as $\Q$-schemes) is naturally isomorphic to $\bar E(\Qbar)$ (mophisms as $\Qbar$-schemes) for a uniquely determined elliptic curve $\bar E/\Qbar$ 26, so the results of the previous (sub)section apply to $E(\Qbar)$. In particular, fixing a prime $\l$, for all $n\ge1$, we have
\[E(\Qbar)[\l^n]=\Zmod{\l^n}\oplus\Zmod{\l^n}.\]Now, note that $G_\Q$ has a natural (left) action on $E(\Qbar)$. Spelled out, given $\Qbar$-point $x:\spec\Qbar\to E$ and an automorphism $\sigma\in G_\Q$, we let $\sigma\cdot x\in E(\Qbar)$ be the composition
\[\spec\Qbar\xto{\spec\sigma}\spec\Qbar\xto xE.\]Since multiplication by $m$ is defined over $\Q$, this action commutes with the multiplication by $m$ map, and so restrictions to a linear action $G_\Q\actson E(\Qbar)[m]$ for all $m\ge1$. Thus, we have compatible maps
\[G_\Q\too\Aut(E(\Qbar)[\l^n])\simeq\Aut\parens{\Zmod{\l^n}\oplus\Zmod{\l^n}}\]for all $n\ge1$. Letting, $T_\l(E):=\invlim_{n\ge1}E(\Qbar)[\l^n]$ be the ($\l$-adic) Tate module and taking an inverse limit of the above maps, we get our desired representation
\[\rho_{E,\l}:G_\Q\too\Aut(T_\l(E))\simeq\Aut(\Z_\l\oplus\Z_\l)\simeq\GL_2(\Z_\l)\into\GL_2(\Q_\l)\]of $G_\Q$.
Assuming I continue this series and things work out roughly the way I hope they do, we will in a later post show that this representation is irreducible most of the time.
-
Not necessarily in this order ↩
-
I feel like I keep semi-accidentally writing super long posts, and I’m not a fan of this (especially this one. It probably did not need to be anywhere near this long) ↩
-
I’ll include exercise. I encourage you to do some (but probably not all) of them just to have practice thinking about this stuff. ↩
-
On the off chance I succeed in writing this post and putting it online, I should mention that you can probably go straight to the part about curves, pretend the word scheme does not exist, and still manage to follow. I hope to make things fairly concrete because then there is less theory I need to remember how to set up ↩
-
The part before elliptic curves is kinda messy right now because of a long series of rewriting it as I realized setting things up would be a more involved process than i anticipated. If you read it, watch out for typos/mistakes (In particular, watch out for places where I’m implicitly assuming a field is algebraically closed when I shouldn’t be). If you find mistakes (or if things are unclear), leave a comment ↩
-
collection of charts ↩
-
All of this data is still there, but now neatly packaged into the structure sheaf $\ints X$ ↩
-
In either case, the morphism of sheaves is not required to have much of anything to do with the map on underlying spaces ↩
-
In the classical setting, $A=k[x_1,\dots,x_n]/\sqrt I$ is a f.g. $k$-algebra and $\spec A$ corresponds to the set $V(I)=\bracks{(a_1,\dots,a_n)\in k^{\oplus n}:f(a_1,\dots,a_n)=0\,\forall f\in I}\subset k^{\oplus n}$, so the global functions on $V(I)=\spec A$ are given by $A=k[x_1,\dots,x_n]/\sqrt I$. ↩
-
Given $\msF\in\Ab(X)$, embed the stalk $\msF_x\into I_x$ into an injective group. For each $x\in X$, let $j_x:{x}\into X$ denote the inclusion, and consider the sheaf $\msI=\prod_{x\in X}j_{x,* }(I_x)$ where $I_x$ is viewed as a sheaf on ${x}$. This is an injective sheaf into which $\msF$ embeds. ↩
-
It’s an (annoying to prove) theorem that cohomology (for the sheaves we care about) vanish in degrees above the dimension of the underlying space ↩
-
Really, I’ll claim without proof ↩
-
I know this notation is trash, but it’s also short-lived ↩
-
Hints: (1) A uniformizer in $\ints{C,p}\subset k(C)$ is like a local coordinate centered at $p$ and (2) the function field $k(C)$ is the stalk at the generic point $\eta\in C$ (i.e. the point contained in all open sets (i.e. the point whose closure is all of $C$ (i.e. the point corresponding to the zero ideal in any affine open))) ↩
-
You may also want to appeal to Nike’s trick: for $\spec A,\spec B\subset X$ affines in a general scheme $X$, we can cover the intersection $\spec A\cap\spec B$ with affines $U$ that are distinguished in both $\spec A,\spec B$ (i.e. $U=\spec A_a\subset\spec A$ and $U=\spec B_b\subset\spec B$ for some $a\in A$ and $b\in B$) ↩
-
Plus all the other stuff I’ve asked you to take for granted ↩
-
For example, if you are working over $\C$ where you have access to topological methods, then $f$ is generally (and I think always) a function of the chern classes of $\msF$ which only see the bundle’s underlying topology (and not its complex/holomorphic structure) ↩
-
This boils down to the fact that the unit ideal $(1)=A$ of a ring $A$ has a finite set of generators. ↩
-
I haven’t thought this through, so I could be wrong, but for curves, the given definition of completeness is the same as being proper. Briefly, Riemann-Roch (+ some work) shows that a complete curve $C$ can be embedded in some projective space $\P_k^N$ (as a closed subset), but projective space is proper and so its closed subsets are too. ↩
-
and also retroactively for some of the earlier stuff (e.g. Serre duality) ↩
-
This it the standard way to label the indices for some reason. I guess note that the index + the valuation of the corresponding monomial always equals 6 ↩
-
I think these are the right substitutions. I haven’t actually checked ↩
-
By Yoneda, to show this, it suffices to give $E(S)$ a (functorial in $S$) group law for all $k$-schemes $S$. I believe, but have not checked, that one can do this by showing that $E(S)$ is in natural bijection with $\Pic^0(E\by_kS)$ where $E\by_kS$ is the (categorical) pullback of $E\to\spec k\from S$.
Actually, I think there’s a slicker way to do this. Maybe I’ll come back and type something up at some point… ↩ -
The middle expression here really shows that I made some poor choices of notation ↩
-
I did not touch on this before, but morphisms between smooth curves are in bijection field maps between their function fields. ↩
-
$\bar E$ is the “base change of $E$ to $\Qbar$”. Intuitively, it results from taking $E/\Q$ and then extending scalars from $\Q$ to $\Qbar$. ↩
